Once again I rediscovered something that I once knew, but had forgotten. Fortunately, this blog is a good place to share little code snippets that I don't want to forget.
I needed to compute the diagonal elements of a product of two matrices. In symbols, I have an nxp matrix, A, and a pxn matrix, B, and I want the vector of values vecdiag(A*B).
Instead of forming the matrix product A*B, which is an O(n2p) operation, I can compute the diagonal value in O(np) computations. The computation (using SAS/IML notation) is (A#B`)[,+]. That is, you compute the elementwise product of A and the transpose of B, and then sum across all rows.
Here's a short example to show that these operations are equivalent:
proc iml; A = rannor( j(6,5) ); /** 5x6 matrix **/ B = rannor( j(5,6) ); /** 6x5 matrix **/ d1 = vecdiag(A*B); d2 = (A#B`)[,+]; print d1 d2; |
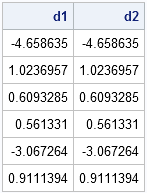
How did I remember that I once knew this little trick but then forgot it? Well, not even a year ago I published essentially the same trick in an article titled "Computing the trace of a product of matrices." That post also has a graph that compares the times required to compute each quantity.

2 Comments
Hi Rick, an alternative way through pattern recognition:
proc iml;
A = rannor( j(6,5) ); /** 5x6 matrix **/
B = rannor( j(5,6) ); /** 6x5 matrix **/
ProdMat = A*B;
Y=ProdMat[do(1, nrow(ProdMat)*ncol(ProdMat), nrow(ProdMat)+1 )]`; /** for a 6*6 matrix, this takes out the 1st, 8th, 15th...36th element which form the diagonal **/
print d3;
Thanks.
Pingback: How to compute Mahalanobis distance in SAS - The DO Loop