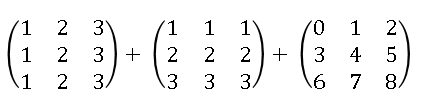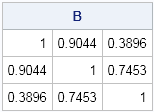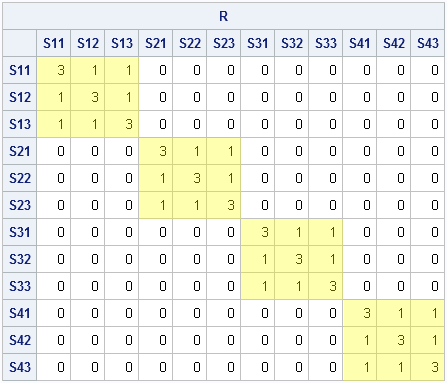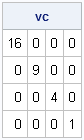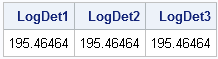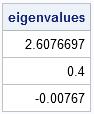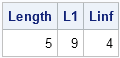
Did you know that SAS/IML 12.1 provides built-in functions that compute the norm of a vector or matrix? A vector norm enables you to compute the length of a vector or the distance between two vectors in SAS. Matrix norms are used in numerical linear algebra to estimate the condition
Recently a SAS/IML programmer asked a question regarding how to perform matrix arithmetic when some of the data are in vectors and other are in matrices. The programmer wanted to add the following matrices: The problem was that the numbers in the first two matrices were stored in vectors. The
For programmers who are learning the SAS/IML language, it is sometimes confusing that there are two kinds of multiplication operators, whereas in the SAS DATA step there is only scalar multiplication. This article describes the multiplication operators in the SAS/IML language and how to use them to perform common tasks
In statistics, distances between observations are used to form clusters, to identify outliers, and to estimate distributions. Distances are used in spatial statistics and in other application areas. There are many ways to define the distance between observations. I have previously written an article that explains Mahalanobis distance, which is
Someone recently asked a question on the SAS Support Communities about estimating parameters in ridge regression. I answered the question by pointing to a matrix formula in the SAS documentation. One of the advantages of the SAS/IML language is that you can implement matrix formulas in a natural way. The
Frequently someone will post a question to the SAS Support Community that says something like this: I am trying to do [statistical task]and SAS issues an error and reports that my correlation matrix is not positive definite. What is going on and how can I complete [the task]? The statistical
The other day I was constructing covariance matrices for simulating data for a mixed model with repeated measurements. I was using the SAS/IML BLOCK function to build up the "R-side" covariance matrix from smaller blocks. The matrix I was constructing was block-diagonal and looked like this: The matrix represents a
I recently encountered a SUGI30 paper by Chuck Kincaid entitled "Guidelines for Selecting the Covariance Structure in Mixed Model Analysis." I think Kincaid does a good job of describing some common covariance structures that are used in mixed models. One of the many uses for SAS/IML is as a language
The determinant of a matrix arises in many statistical computations, such as in estimating parameters that fit a distribution to multivariate data. For example, if you are using a log-likelihood function to fit a multivariate normal distribution, the formula for the log-likelihood involves the expression log(det(Σ)), where Σ is the
This article is an excerpt from my forthcoming book Simulating Data with SAS. Not every matrix with 1 on the diagonal and off-diagonal elements in the range [–1, 1] is a valid correlation matrix. A correlation matrix has a special property known as positive semidefiniteness. All correlation matrices are positive
