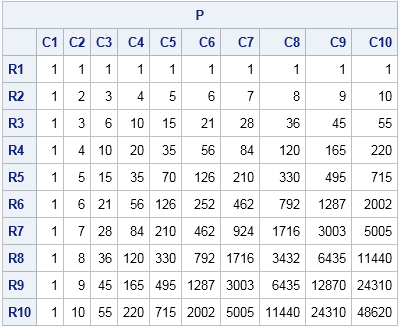
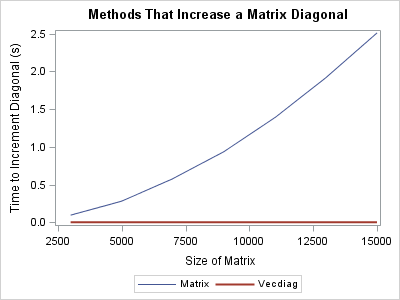
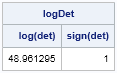
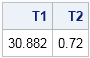
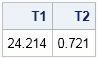
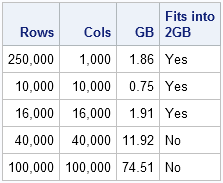
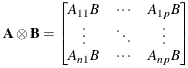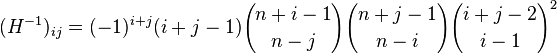I began 2015 by compiling a list of popular articles from my blog in 2014. Although this "People's Choice" list contains many interesting articles, some of my favorites did not make the list. Today I present the "Editor's Choice" list of articles that deserve a second look. I've highlighted one