Dear Rick,
I am trying to create a numerical matrix with 100,000 rows and columns in PROC IML. I get the following error:
(execution) Unable to allocate sufficient memory.
Can IML allocate a matrix of this size? What is wrong?
Several times a month I see a variation of this question. The numbers vary. Sometimes it is 250,000 or one million rows. Sometimes the matrix is not square, but it is always big.
The IML procedure holds all matrices in RAM, so whenever I see this question I compute how much RAM is required for the specified matrix. Each element in a double-precision numerical matrix requires eight bytes. Therefore, if you know the size of a matrix, you can write a simple formula that computes the gigabytes (GB) of RAM required to hold the matrix in memory.
There are two definitions of a gigabyte. Disk drives and storage devices use 1 GB to mean 109 bytes. However, the historical definition in computer science is 10243 = 230 bytes, which is 1.07 x 109. These competing definitions are sufficiently close that you don't usually have to worry about the difference. For back-of-the envelope computations I use the simpler formula: an r x c matrix double-precision matrix requires r*c*8/109 gigabytes of RAM.
Because RAM is traditionally measured by using the second definition, the following SAS/IML module accurately calculates the number of gigabytes of RAM (using the computer science definition) required to hold a matrix of a given dimension:
proc iml;
/* Compute gigabytes (GB) of RAM required for matrix with r rows and c columns */
start HowManyGigaBytes(Rows, Cols);
GB = 8 # Rows#Cols / 2##30; /* 1024##3 bytes in a gigabyte */
Fit2GB = choose(GB <= 2, "Yes", " No");
print Rows[F=COMMA9.] Cols[F=COMMA9.]
GB[F=6.2] Fit2GB[L="Fits into 2GB"];
finish;
/* test: rows cols */
sizes = {250000 1000,
10000 10000,
16000 16000,
40000 40000,
100000 100000 };
run HowManyGigaBytes(sizes[,1], sizes[,2]); |
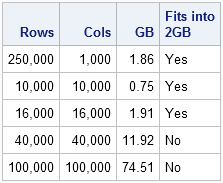
You can see from the table that a square matrix with dimension 100,000 requires 74.5 GB of RAM when stored as a dense matrix. A typical "off-the-shelf" laptop or desktop computer might have 4 or 8 GB of RAM, but of course some of that is used by the operating system.
Usually you need to hold several matrices in RAM in order to add or multiply them together. The last column in the table indicates whether the specified matrix dimensions can fit into 2 GB of RAM, which is a convenient proxy for the practical question, "how big can my matrices be if I want to operate with several at once." Of course, the definition of "several" will depend on whether your computer has 8 GB, 16 GB, or more RAM. For square matrices, a matrix of size 16,000 will fit into 2 GB of RAM.
Because 2 GB is a useful benchmark and because not all matrices are square, the following statements show the dimensions of some non-square matrices that also fit into 2 GB:
rows = 1000 * ({5 10 16} || do(20, 100, 20));
colsPerGB = 2##30 / 8 / rows;
cols = floor( 2 * colsPerGB ); /* columns for 2 GB */
print (rows // cols)[F=comma10. R={"Rows" "Cols"}
L="Matrices that Fit into 2 GB RAM"]; |

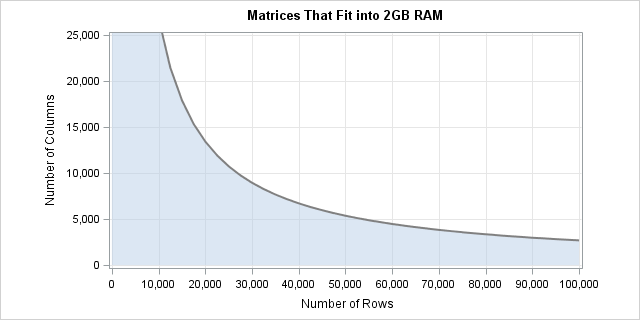
You can compute more values in this fashion and use PROC SGPLOT to create a graph that shows the dimensions of matrices that fit into 2 GB of RAM. The vertical axis of the following image has been truncated at 25,000 columns. (Click to enlarge.) The full graph is symmetric about the identity line because a matrix and its transpose contain the same number of columns.
In conclusion, it is useful to be able to calculate how many gigabytes of storage a matrix requires. In SAS/IML, if you intend to compute with several matrices, they must collectively fit into RAM. I have provided some simple computations that enable you to quickly check whether your matrices fit into 2 GB of RAM. You can, of course, modify the program to find matrices that fit into 1 GB, 0.5 GB, or any other size.

4 Comments
Pingback: Big data problems for Criminal Justice | Andrew Wheeler
Pingback: Large matrices in SAS/IML 14.1 - The DO Loop
Pingback: Compute nearest neighbors in SAS - The DO Loop
Pingback: Large matrices in SAS/IML - The DO Loop