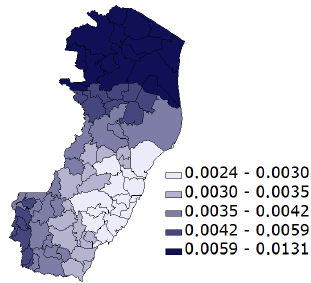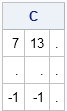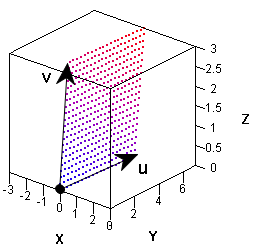
A grid is a set of evenly spaced points. You can use SAS to create a grid of points on an interval, in a rectangular region in the plane, or even in higher-dimensional regions like the parallelepiped shown at the left, which is generated by three vectors. You can use
Children in primary school learn that every positive number has a real square root. The number x is a square root of s, if x2 = s. Did you know that matrices can also have square roots? For certain matrices S, you can find another matrix X such that X*X
Last week I attended SAS Global Forum 2016 in Las Vegas. I and more than 5,000 other attendees discussed and shared tips about data analysis and statistics. Naturally, I attended many presentations that featured using SAS/IML software to implement advanced analytical algorithms. Several speakers showed impressive mastery of SAS/IML programming
Last week I showed how to create dummy variables in SAS by using the GLMMOD procedure. The procedure enables you to create design matrices that encode continuous variables, categorical variables, and their interactions. You can use dummy variables to replace categorical variables in procedures that do not support a CLASS
I began 2016 by compiling a list of popular articles from my blog in 2015. This "People's Choice" list contains many interesting articles, but some of my personal favorites did not make the list. Today I present the "Editor's Choice" list of articles that deserve a second look. I've grouped
A recent question posted on a discussion forum discussed storing the strictly upper-triangular portion of a correlation matrix. Suppose that you have a correlation matrix like the following: proc iml; corr = {1.0 0.6 0.5 0.4, 0.6 1.0 0.3 0.2, 0.5 0.3 1.0 0.1, 0.4 0.2 0.1 1.0}; Every correlation
You've had a long day. You've implemented a custom algorithm in the SAS/IML language. But before you go home, you want to generate some matrices and test your program. If you are like me, you prefer a short statement—one line would be best. However, you also want the flexibility to
Occasionally a SAS statistical programmer will ask me, "How can I construct a large correlation matrix?" Often they are simulating data with SAS or developing a matrix algorithm that involves a correlation matrix. Typically they want a correlation matrix that is too large to input by hand, such as a
Suppose that you compute the correlation matrix (call it R1) for a set of variables x1, x2, ..., x8. For some reason, you later want to compute the correlation matrix for the variables in a different order, maybe x2, x1, x7,..., x6. Do you need to go back to the
Sometimes I get contacted by SAS/IML programmers who discover that the SAS/IML language does not provide built-in support for multiplication of matrices that have missing values. (SAS/IML does support elementwise operations with missing values.) I usually respond by asking what they are trying to accomplish, because mathematically matrix multiplication with
