In statistics, distances between observations are used to form clusters, to identify outliers, and to estimate distributions. Distances are used in spatial statistics and in other application areas.
There are many ways to define the distance between observations. I have previously written an article that explains Mahalanobis distance, which is used often in multivariate analysis, and I have showed how to compute the Mahalanobis distance in SAS. Today's article is simpler: how do you compute the usual Euclidean distance in SAS?
Recall that the squared Euclidean distance between the point p = (p1, p2, ..., pn) and the point q = (q1, q2, ..., qn) is the sum of the squares of the differences between the components: Dist2(p,q) = Σi (pi – qi)2. The Euclidean distance is then the square root of Dist2(p,q). This article shows three ways to compute the Euclidean distance in SAS:
- By using the DISTANCE procedure in SAS/STAT software.
- By using the DISTANCE function in SAS/IML software.
- By writing your own SAS/IML function.
The following DATA step creates 27 observations that are arranged on an integer lattice in three dimensions. Each row of the data set contains an observation in three variables. The 27 points are (0,0,0), (0,0,1), (0,0,2), (0,1,0), ..., (2,2,2).
data Obs; do x=0 to 2; do y=0 to 2; do z = 0 to 2; output; end; end; end; run; |
Compute distance by using SAS/STAT software
PROC DISTANCE can compute many kinds of distance, and can also standardize the data variables, which is useful when your variable represent different quantities (such as height, weight, and age). In the simple case of Euclidean distance without any standardization, specify the METHOD=EUCLID option and the NOSTD option on the PROC DISTANCE statement, as follows:
proc distance data=Obs out=Dist method=Euclid nostd; var interval(x y z); run; proc print data=Dist(obs=4); format Dist: 8.6; var Dist1-Dist4; run; |
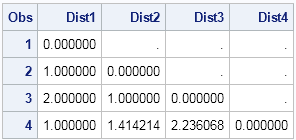
The output data set has 27 variables and 27 observations. The preceding table shows the first four observations and the first four variables. You can see that the output data set is the lower-triangular portion of the distance matrix. The ith row gives the distance between the ith observation and the jth observation for j ≤ i. For example, the distance between the fourth observation (0,1,0) and the second observation (0,0,1) is sqrt(02 + 12 + 12)= sqrt(2) = 1.414.
If you prefer to output the full, dense, symmetric matrix of distances, use the SHAPE=SQUARE option on the PROC DISTANCE statement.
Compute distance in SAS/IML Software
In SAS/IML software, you can use the DISTANCE function in SAS/IML to compute a variety of distance matrices. The DISTANCE function was introduced in SAS/IML 12.1 (SAS 9.3M2).
By default, the DISTANCE function computes the Euclidean distance, and the output is always a square matrix. Therefore, the following statements compute the Euclidean pairwise distances between the 27 points in the Obs data set:
proc iml;
use Obs;
read all var _NUM_ into X;
close Obs;
D = distance(X);
print (D[1:4, 1:4])[format=8.6 c=("Dist1":"Dist4")]; |
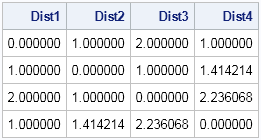
The output shows that the values in the upper-left portion of the distance matrix are the same as were computed by PROC DISTANCE.
How to compute pairwise distance in SAS
Sometimes you do not want to compute the complete matrix of pairwise distances between observations. Sometimes you only need the distances between observations that belong to different groups. For example, you might have one set of locations that represent warehouses and another set that represents the locations of retail stores. You might be interested in computing the distances from each store to the warehouses, so that you can efficiently ship goods to each store from the closest warehouse.
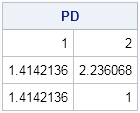
In SAS/IML 14.3 (released as part of SAS 9.4M5), the DISTANCE function in PROC IML can compute pairwise distances between points in two groups. For example, the following computes a 3 x 2 matrix of the distances between three points in the "P group" and two points in the "Q group":
p = { 1 0, 1 1, -1 -1}; q = { 0 0, -1 0}; PD = distance(p,q); /* SAS/IML 14.3 */ print PD[r=("p1":"p3") c=("q1":"q2") ]; |
If you do not have access to SAS/IML 14.3, the following SAS/IML module computes the distances between observations in the matrix X and the matrix Y. The (i,j)th element of the result is the distance between the ith row of X and the jth row of Y.
/* compute Euclidean distance between points in x and points in y.
x is a n x d matrix, where each row is a point in d dimensions.
y is a m x d matrix.
The function returns the n x q matrix of distances, D, such that
D[i,j] is the distance between x[i,] and y[j,]. */
start PairwiseDist(x, y);
if ncol(x)^=ncol(y) then return (.); /* different dimensions */
n = nrow(x); m = nrow(y);
idx = T(repeat(1:n, m)); /* index matrix for x */
jdx = shape(repeat(1:m, n), n); /* index matrix for y */
diff = X[idx,] - Y[jdx,];
return( shape( sqrt(diff[,##]), n ) ); /* sqrt(sum of squares) */
finish;
p = { 1 0,
1 1,
-1 -1};
q = { 0 0,
-1 0};
PD = PairwiseDist(p,q);
print PD; |
If you are still running SAS/IML 9.3 or earlier, you can also use the PairwiseDist function to define your own function that computes the Euclidean distance between rows of a matrix:
/* compute Euclidean distance between points in x.
x is a p x d matrix, where each row is a point in d dimensions.
Use the DISTANCE function in SAS/IML 12.1 and later releases. */
start EuclideanDistance(x);
y=x;
return( PairwiseDist(x,y) );
finish;
D = EuclideanDistance(X);
print (D[1:4, 1:4])[format=8.6 c=("Dist1":"Dist4")]; |
The output is the same as for the built-in DISTANCE function, and is not printed.

7 Comments
Pingback: 13 popular articles from 2013 - The DO Loop
Pingback: Compute nearest neighbors in SAS - The DO Loop
Pingback: Distances between observations in two groups - The DO Loop
Hello,
I'm looking at calculating a distance matrix in SAS using Yule's Q.
It would be very helpful if you could assist me with the same
Thanks and Regards
Mari
You can ask questions, post data and code, and get advice at the SAS Statistical Community.
Warehouse/Stores seems like a common problem to solve. I assume you have load the Y matrix of stores similarly (read all var _NUM_ into Y;). How to you actually figure out which store should be supplied by which warehouse. Is there a way to use ID variables? Can you show the full code with this example?
The comments of a blog post are not ideal for posting code, so post sample data and the program you've written so far to the SAS/IML Support Community. Someone will be able to help you figure out how to complete the program.