The birthday-matching problem (also called the birthday paradox or simply the birthday problem), is a classic problem in probability. Simply stated, the birthday-matching problem asks, "If there are N people in a room, what is the chance that two of them have the same birthday?" The problem is sometimes called a "paradox" because the chance of a shared birthday is more than 50% when there are N=23 people in a room, which seems like a surprisingly small number of people considering that there are 365 possible birthdays.

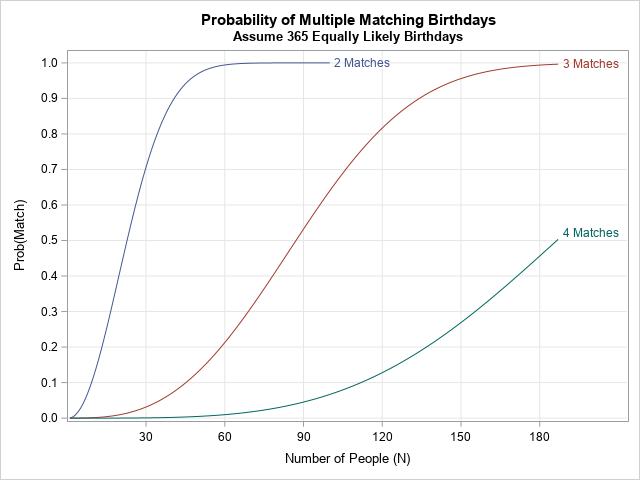
A previous article shows a formula that computes the exact probability for any value of N, assuming a uniform distribution of 365 birthdays. "Sharing a birthday" is called "a collision" in other contexts, as explained in the next section. This article discusses the generalized birthday problem and implements a generalized formula for the probability that there are D collision among N items, when each item has an attribute that is uniformly distributed among C categories. For the classic birthday paradox, D=2 and C=365. The probabilities in the birthday problem can be summarized by using a graph. For each sample size (N), what is the probability of D matches? The graph at the right shows curves for D=2, 3, and 4 when there are C = 365 categories.

The Wikipedia article on the birthday problem contains other possible generalizations.

Ways to generalize the birthday-matching problem

One way to generalize the birthday problem is to think of "the number of birthdays" as a parameter. Let C be the number of categories in the attribute that each subject shares. In the classical birthday paradox, C = 365. However, you can use the same formula to ask whether any subject shares the same "birthday month" (C = 12) or "day-of-the-month birthday" (C = 30). Moreover, the same formula determines the probability that any pair of N six-sided dice share the same value (C = 6). When C ≠ 365, the problem is called the "collision problem." This generalization is used to compute the probability of a collision (a repeated value) in a random sample where each item is uniformly distributed at random among C values.

A second way to generalize the birthday problem is to think of "the number of duplicates" as a parameter. Let D be the number of subjects who must share a value of an attribute. Equivalently, D is the "number of collisions" that we want to observe. In the classic birthday paradox, D = 2. However, you can ask whether D = 3 or D = 4 people share a common birthday. In this case, the classic computational formula that works for D = 2 is no longer valid. However, Diaconis, P. and Mosteller F. (1989, "Methods for studying coincidences", JASA) published an approximation (Eqn 7.5 on p. 857) that works for arbitrary values of D. The approximation is best when the probability of a collision is not too small.

The generalized birthday problem in SAS

The following SAS IML program implements the generalized birthday problem in SAS. It enables you to compute the probability that there are D collision among N items, when each item has an attribute that is uniformly distributed among C categories. For the classic birthday paradox, D=2 and C=365. The method uses the formula of Diaconis and Mosteller (Eqn 7.5 on p. 857) to approximate the cumulative probability. Notice that the probability might be very small for some values of the parameters and depends on an expression of the form (1 - exp(·)). If you are not careful, a simple evaluation of the function x → 1 – exp(x) can lose accuracy when x is very small. SAS supports the EXPM1 function as of the 23.11 Release of SAS Viya. However, for readers who are using SAS 9 or an earlier version of SAS Viya, the following program implements a function called EXPM that carefully evaluates the function.

proc iml;
/* evaluate y=exp(x)-1 accurately when x is near 0.
   See https://blogs.sas.com/content/iml/2023/10/16/expxm1.html 
   SAS supports the built-in EXPM1 function as of the 23.11 Release of SAS Viya.
*/
start expm1(x);
   if abs(x) > 0.03 then return( exp(x)-1.0 );
   /* approximate by using a Taylor polynomial */
   Taylor = x*( 1 + x/2*(1 + x/3*(1 + x/4*(1 + x/5*(1 + x/6)))) );
   return( Taylor );
finish;
 
/* The generalized birthday problem:
   In a room that contains N people who have equal probability of 
   belonging to nCat different categories, 
   return the probability that nDup people share a category.
   The classic birthday problem is nCat=365 and nDup=2.
*/
start CDFBirthday(N, nCat=365, nDup=2);
   if nDup < 2 then return(1.0);          /* everyone shares a BDay with themselves */
   if nDup > N then return(0.0);          /* can't have nDup matches if there aren't that many people! */
   if N > nCat*(nDup-1) then return(1.0); /* Ex: If N>365, there must be a shared BDay */
   /* For NDup=2, use an explicit formula. See
      https://blogs.sas.com/content/iml/2012/04/09/vectorized-computations-and-the-birthday-matching-problem.html
   */
   if nDup = 2 then do;
      i = 1:N;             /* enumerate the N individuals */
      iQ = 1 - (i-1)/nCat; /* individual probabilities */
      Q = prod(iQ);        /* compute probability of "no match" for N people */
      return(1 - Q);       /* prob of a match */
   end;
   /* Otherwise, use formula (Eqn 7.5 on p. 857) of
      Diaconis, P. and Mosteller F. (1989)
      See also the pbirthday function in R, which implements the formula. */
   k = nDup; c=NCat;                 /* for brevity, change notation */
   LHS = N * exp(-N/(c*k)) / (1 - N/(c*(k+1)))##(1/k);
   /* take log of both sides and solve for log(-log(1-p)) */
   LmL1mp = k*log(LHS) - (k-1)*log(c) - lgamma(k+1);
   /* now solve for p in y=log(-log(1-p)).
      Note: use of EXPM1 function in case of small probabilities */
   return( -expm1(-exp(LmL1mp)) );   /* = 1.0 - exp(-exp(LmL1mp)) */
finish;

In this function, the classic case where nDup=2 is handled first. If nDup > 2, the function uses the Diaconis-Mosteller approximation. Let's run the function on a few examples:

/* some tests for evaluating the birthday CDF */
Prob2BDay  = CDFbirthday(23);           * N=23, nCat=365, nDup=2;
Prob3BDay = CDFBirthday(23,  365, 3);   * N=23, nCat=365, nDup=3;
EquiProb3 = CDFBirthday(88,  365, 3);   * N=88, nCat=365, nDup=3;
EquiProb4 = CDFBirthday(187, 365, 4);   * N=187, nCat=365, nDup=4;
print Prob2BDay Prob3BDay EquiProb3 EquiProb4;

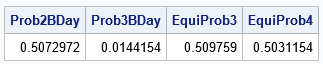
The output shows the probabilities associated with the following situations:

• In a room that contains 23 people, what is the probability of a shared birthday, assuming the (default) values nCat=365 and nDup=2? This is the classic birthday paradox: the chance is greater than 50%.
• In the same room, what is the probability that three or more people share a birthday? Clearly, the probability is much less.
• What is the probability that three or more people share a birthday in a group of 88? This is the "birthday paradox" for nDup=3. In a group of 88, the chance is greater than 50% that three people share a birthday.
• What if we ask about four people sharing a birthday? Now you need a group of 187 before the chance is greater than 50%.

We can also ask about sharing birth months (C=12) or sharing a birth day-of-the-month (C=30):

/* if N=23, what is the probability that three or more share a birth month?
   What about a birth day-of-month (eg, the 16th or some month) */
Prob3Month = CDFBirthday(23, 12, 3);        * N=23, nCat=12, nDup=3;
Prob3DayOfMonth = CDFBirthday(23, 30, 3);   * N=23, nCat=30, nDup=3;
print Prob3Month Prob3DayOfMonth;

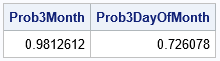
The computation shows that in a room that contains N=23 people, there is a 98% chance that three people share a birth month (for example, born in September). There is almost a 73% chance that three people have a birthday on the same day-of-the-month (for example, the 16th of December, the 16th of April, and the 16th of October). These probabilities are approximations. The computation assumes that birthdays are evenly distributed across months and across the days 1–30.

The graph of the collision probability

By using the CDF function for the birthday probability, you can compare the probabilities of matching nDup birthdays for nDup=2, 3, 4, .... The following program computes the CDF function for the generalized birthday problem, which shows the probability of 2, 3, and 4 people having a shared birthday within groups of various sizes:

/* compute probability for multiple values of nDup */
N = T(1:187);
CDF = j(nrow(N), 3, .);
do nDup = 2 to 4;
   if nDup=2 then max=100; else max=nrow(N);
   do i = 1 to max;
      CDF[i,nDup-1] = CDFBirthday(N[i], 365, nDup); * nCat=365;
   end;
end;
 
create CDF from N CDF[c={'N' 'CDF2' 'CDF3' 'CDF4'}];
append from N CDF;
close;
 
submit;
title "Probability of Multiple Matching Birthdays";
title2 "Assume 365 Equally Likely Birthdays";
proc sgplot data=CDF;
   series x=N y=CDF2 / curvelabel="2 Matches";
   series x=N y=CDF3 / curvelabel="3 Matches";
   series x=N y=CDF4 / curvelabel="4 Matches";
   xaxis grid label="Number of People (N)" values=(0 to 180 by 30) valueshint;
   yaxis grid label="Prob(Match)" values=(0 to 1 by 0.1);
run;
endsubmit;

The graph is shown at the top of this article. The graph shows that the probability of a shared birthday between two people is greater than 50% when there are 23 people in a room, and it rises to near certainty for 60 people. In contrast, if you want three people to share a birthday, the probability exceeds 50% when there are 87 people, and it is nearly certain when there are 180 people. Lastly, if you want four people to share a birthday, the probability exceeds 50% when there are 188 people.

Summary

The generalized birthday problem is also called the collision problem. If you want the probability that at least two people (in a group of N) share a common attribute, there is an explicit formula. If you want the probability that at least 3 (or 4 or more) people share an attribute, you can approximate the probability. This article implements a SAS IML function that approximates the probability for the generalized birthday problem.

This computation gives you the probability of a collision when you specify the number of people in a group. Often, we are interested in the inverse problem: Specify the probability of a collision and compute how many people we need before the probability of a collision is as specified. This requires that we invert the CDF function to obtain the quantile function. The next article implements the quantile function for the generalized birthday problem.