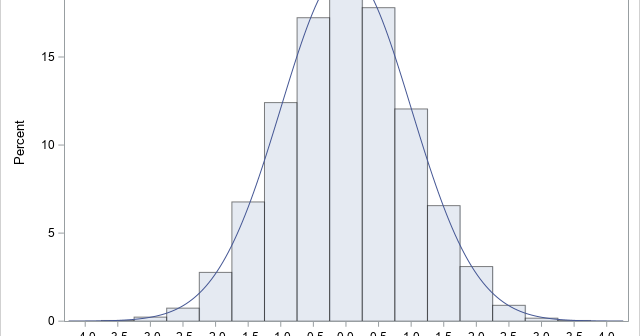
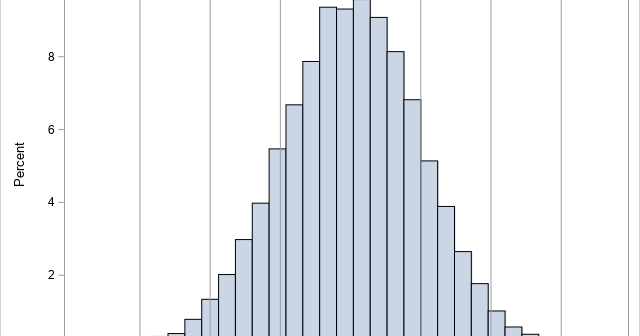
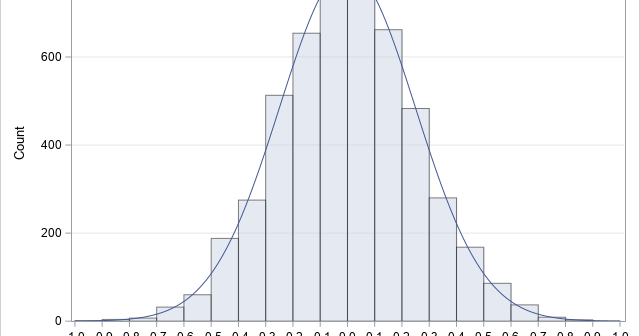
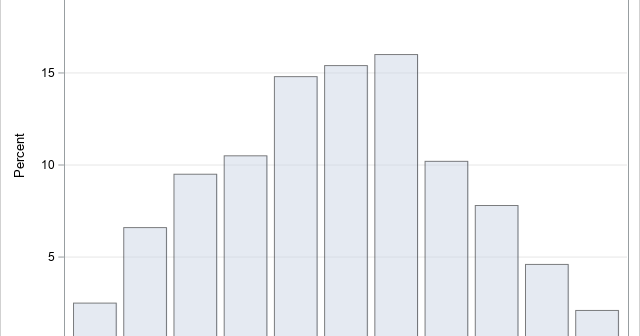
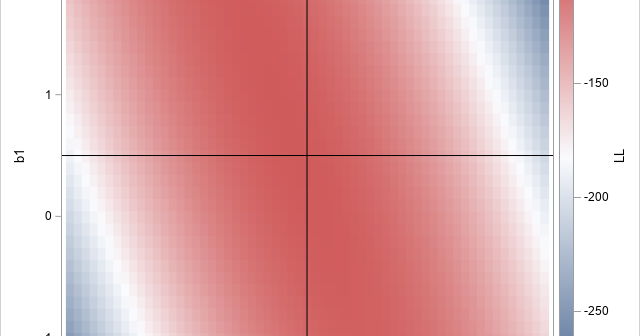
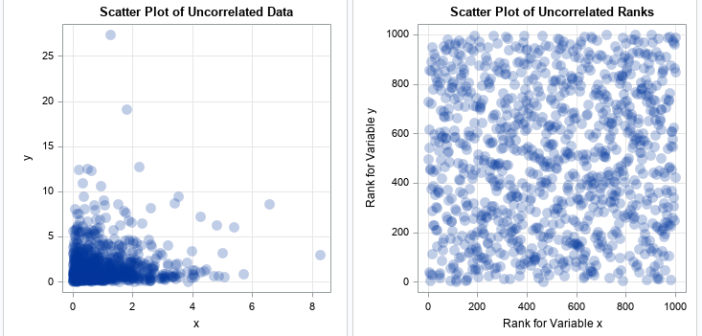
Nearly every statistician has heard the aphorism, "All models are wrong, but some are useful." The quote is attributed to George Box, an early and influential thinker about statistics. Did George Box actually say this quote? Yes, he did. The first part of the quote ("All models are wrong") appeared