Rick Wicklin, PhD, is a distinguished researcher in computational statistics at SAS and is a principal developer of SAS/IML software. His areas of expertise include computational statistics, simulation, statistical graphics, and modern methods in statistical data analysis. Rick is author of the books Statistical Programming with SAS/IML Software and Simulating Data with SAS.
After reading my article about how to use BY-group processing to run 1000 regression models, a SAS programmer asked whether it is possible to reorder the output of a BY-group analysis. The answer is yes: you can use the DOCUMENT procedure to replay a portion of your output in any
Monte Carlo techniques have many applications, but a primary application is to approximate the probability that some event occurs. The idea is to simulate data from the population and count the proportion of times that the event occurs in the simulated data. For continuous univariate distributions, the probability of an
Longtime SAS programmers know that the SAS DATA step and SAS procedures are very tolerant of typographical errors. You can misspell most keywords and SAS will "guess" what you mean. For example, if you mistype "PROC" as "PRC," SAS will run the program but write a warning to the log:
Sometimes SAS programmers ask about how to analyze quantiles with SAS. Common questions include: How can I compute 95% confidence intervals for a median in SAS? How can I test whether the medians of two independent samples are significantly different? How can I repeat the previous analyses with other percentiles,
Many introductory courses in probability and statistics encourage students to collect and analyze real data. A popular experiment in categorical data analysis is to give students a bag of M&M® candies and ask them to estimate the proportion of colors in the population from the sample data. In some classes,
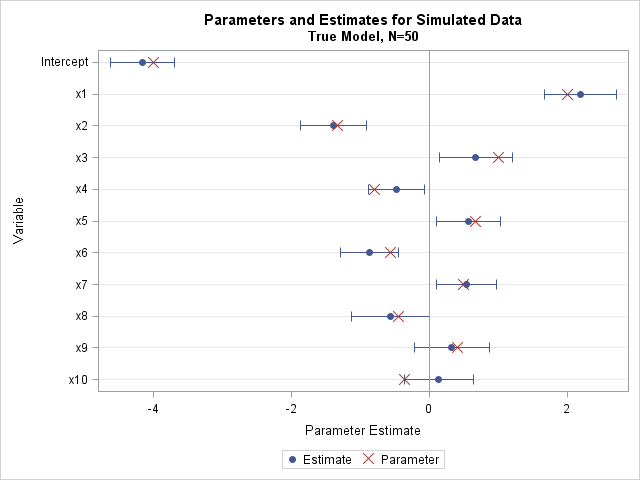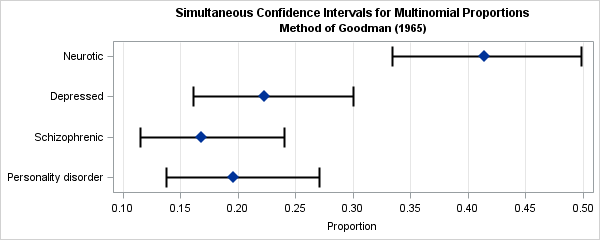
A categorical response variable can take on k different values. If you have a random sample from a multinomial response, the sample proportions estimate the proportion of each category in the population. This article describes how to construct simultaneous confidence intervals for the proportions as described in the 1997 paper
A common question on SAS discussion forums is how to repeat an analysis multiple times. Most programmers know that the most efficient way to analyze one model across many subsets of the data (perhaps each country or each state) is to sort the data and use a BY statement to
On discussion forums, I often see questions that ask how to Winsorize variables in SAS. For example, here are some typical questions from the SAS Support Community: I want an efficient way of replacing (upper) extreme values with (95th) percentile. I have a data set with around 600 variables and
Suppose you create a scatter plot in SAS with PROC SGPLOT. What color does PROC SGPLOT use for the markers? If you specify the GROUP= option so that markers are colored by a grouping variable, what colors are used to represent the various groups? The following scatter plot shows the
In a previous article, I showed how to simulate data for a linear regression model with an arbitrary number of continuous explanatory variables. To keep the discussion simple, I simulated a single sample with N observations and p variables. However, to use Monte Carlo methods to approximate the sampling distribution
