Rick Wicklin, PhD, is a distinguished researcher in computational statistics at SAS and is a principal developer of SAS/IML software. His areas of expertise include computational statistics, simulation, statistical graphics, and modern methods in statistical data analysis. Rick is author of the books Statistical Programming with SAS/IML Software and Simulating Data with SAS.
I got an email asking the following question: In the following program, I don't know how many variables are in the data set A. However, I do know that the variable names are X1–Xk for some value of k. How can I read them all into a SAS/IML matrix when
I have previously written about how to create funnel plots in SAS software. A funnel plot is a way to compare the aggregated performance of many groups without ranking them. The groups can be states, counties, schools, hospitals, doctors, airlines, and so forth. A funnel plot graphs a performance metric
Here's a quick tip to keep in mind when you write SAS/IML programs: although the SAS/IML documentation lists about 300 functions that are built into the SAS/IML language, you can also call hundreds of functions in Base SAS. Furthermore, you can pass in SAS/IML vectors for arguments to the functions.
Halloween night was rainy, so many fewer kids knocked on the door than usual. Consequently, I'm left with a big bucket of undistributed candy. One evening as I treated myself to a mouthful of tooth decay, I chanced to open a package of Wonka® Bottle Caps. The package contained three
Did you know that you can define "abbreviations" in the SAS enhanced editor? These handy little shortcuts can save you a lot of typing. For example, I have an abbreviation for the string _iml. Whenever I type _iml, the editor prompts me to replace those four characters with the following
Here is a little trick to file away. Given a row vector of zeros and ones, thought of as representing a number in base 2, the following SAS/IML statements compute the decimal value of that vector. proc iml; x = {1 0 0 1 1 1}; /* number in base
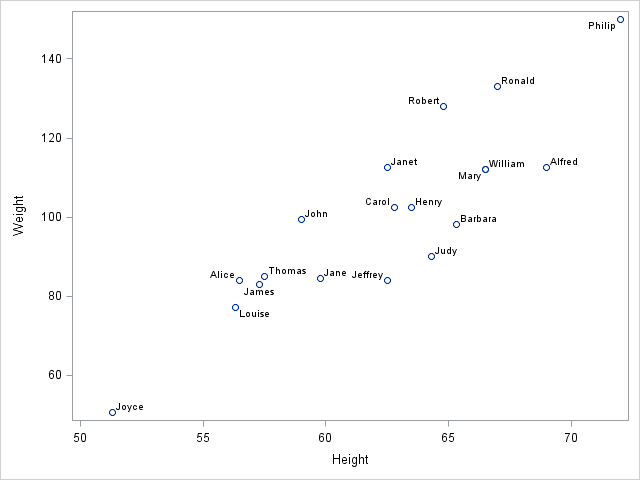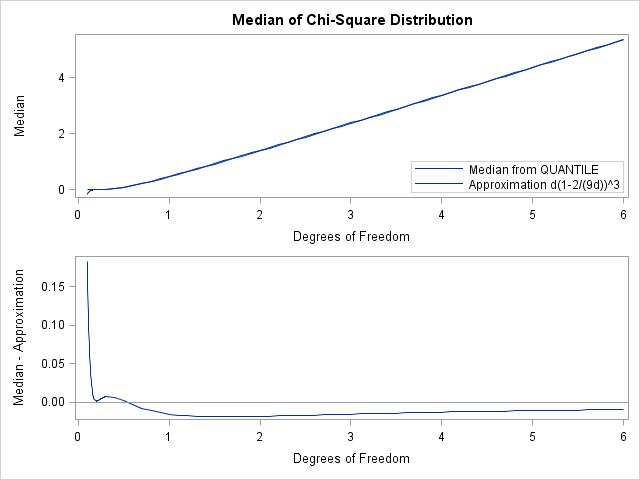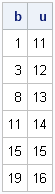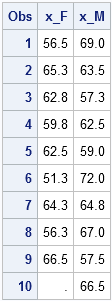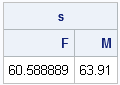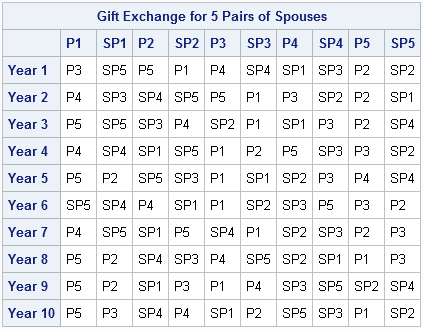
One aspect of blogging that I enjoy is getting feedback from readers. Usually I get statistical or programming questions, but every so often I receive a comment from someone who stumbled across a blog post by way of an internet search. This morning I received the following delightful comment on
If you want to extract values from a SAS/IML vector, use the subscripting operation, such as in the following example: proc iml; x = {A B C D E}; y = x[{1 2 3}]; /* {A,B,C} */ The vector y contains the first three elements of x. However, did you
Sometimes you want to label only certain observations in a plot. This is useful in many ways, but one use is to label outliers on a scatter plot. In the SGPLOT procedure, the DATALABEL= option enables you to specify the name of a variable that is used to label observations.
I was at the Wikipedia site the other day, looking up properties of the Chi-square distribution. I noticed that the formula for the median of the chi-square distribution with d degrees of freedom is given as ≈ d(1-2/(9d))3. However, there is no mention of how well this formula approximates the
