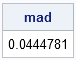
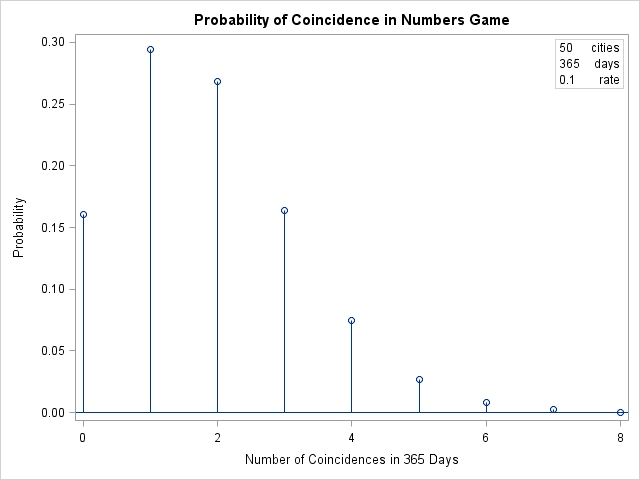
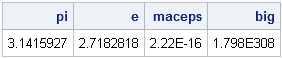
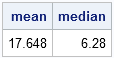
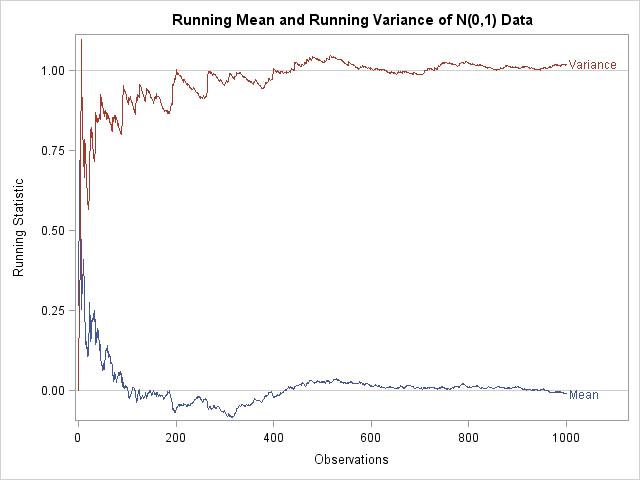
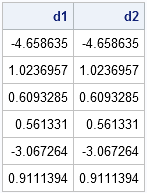
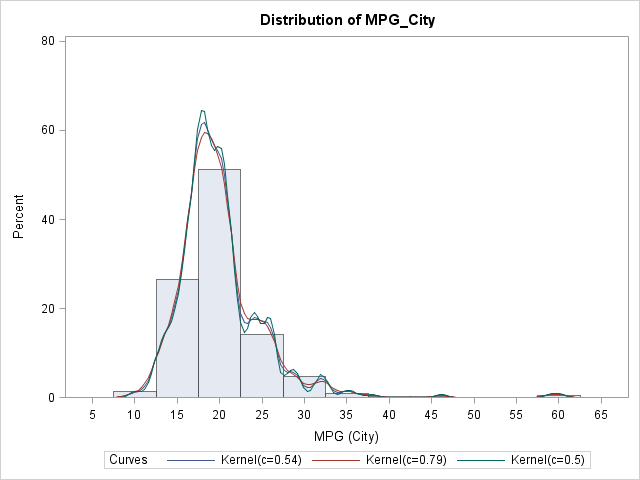
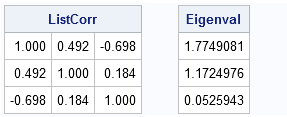
The other day I encountered the following SAS DATA step for generating three normally distributed variables. Study it, and see if you can discover what is unnecessary (and misleading!) about this program: data points; drop i; do i=1 to 10; x=rannor(34343); y=rannor(12345); z=rannor(54321); output; end; run; The program creates the