Happy Pi Day! Every year on March 14th (written 3/14 in the US), people in the mathematical sciences celebrate "all things pi-related" because 3.14 is the three-decimal approximation to π ≈ 3.14159265358979.... The purpose of this day is to have fun, celebrate the importance of mathematics, and maybe learn a little bit about math.
I don't think any number is more fun than π, but I recently saw a post on social media about ππ, which is "pi to the power of pi." Depending on your background and your comfort with math, the number either looks scary or fascinating. This article starts with a quick look at the number ππ. But because mathematicians always want to generalize things, the number ππ motivates me to discuss three "truism" in computational mathematics that are important all year long, and not just on Pi Day:
- Always use critical thinking when you see a mathematical "fact" on the internet.
- Many problems are amenable to general-purpose computational tools, but if a special-purpose function or numerical tool applies, the special-purpose tool is usually faster and more accurate.
- If an equation involves an expression that grows very large, consider log-transforming the equation, which can result in a solution that has better accuracy.
Pi to the pi is 36.462...
At first glance, ππ is no more interesting than 33 or 44. You can type ππ into a calculator to find that its value is approximately 36.462159607.... It is uninteresting, right? Well, maybe yes and maybe no! Mathematicians always want to generalize things, so let's look a little closer at some related ideas.
An infinite series representation? No!
I started thinking about ππ when I saw an image on social media that represented ππ by using the following infinite series:
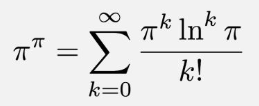
"What madness is this?" I thought. This equation seemed bizarre. My confusion soon turned to annoyance when I realized that I had been deceived. I was a victim of obfuscation. Obfuscation is when someone intentionally makes something simple seem confusing and complex. The social media post is an obfuscation because the author used three elementary mathematical definitions to make something simple look complex:
- By the inverse relationship between logarithms and exponentials, every positive number, y, can be written as \( y = e^{\log(y)}\). For this example, \(\pi^\pi = \exp( \log(\pi^\pi) )\).
- By the power rule of logarithms, \(\log(\pi^\pi) = \pi \log(\pi)\).
- The Taylor series expansion of the exponential function is \( e^x = \sum_{k=0}^{\infty} \frac{x^k}{k!}\)
Consequently, the complicated formula is nothing more than set of identities that were chosen to obfuscate the number ππ. For ANY positive number a and any number b, you can write the identity \(a^b = \sum_{k=0}^{\infty} \frac{b^k \ln^k a}{k!}\). So the equation has NOTHING to do with π!
The intersection of a power function and an exponential function
Is there anything interesting about ππ? At the risk of being accused of obfuscation myself, I think ππ naturally leads us to consider two elementary and familiar mathematical functions: the power function f(x) = xπ and the exponential function g(x) = πx. The number ππ is an obvious solution to the equation f(x) = g(x). You can graph the two functions and see that they intersect at ππ.

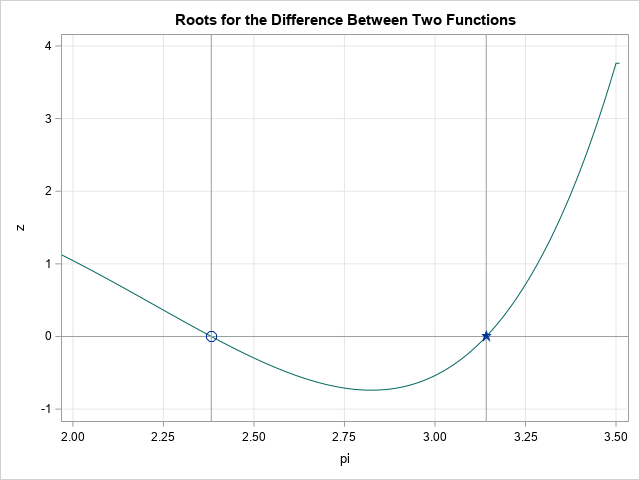
But wait! It looks like the graphs also intersect at a second point in the interval [2, 2.5]. That is, the equation f(x) = g(x) has a second solution. This is apparent when you plot the difference f(x) - g(x) and see that there are two values for which the difference equals 0. One is at x=π ≈ 3.14; the other appears to be close to x = 2.38. Where does this second root come from? Is it related to π? Read on to find out.
The Lambert W function
You can use a standard general-purpose root-finding algorithm to find the two roots of the equation f(x) - g(x) = 0. However, root-finding methods are iterative methods that converge to an approximate solution. Before using an iterative method, it is useful to consider whether you can solve the problem by using a direct method. Usually, direct methods are faster and more accurate than iterative methods. They can also provide more insight.
It turns out that the roots of f(x) - g(x) have an explicit solution in terms of the Lambert W function, which is a direct method that solves equations of the form x*exp(x) = C for x in terms of the right-hand-side constant, C. Although the equation xπ = πx does not initially seem to be the form required to use Lambert's equation, you can manipulate the equations to see the connection.
First, take logarithms of both sides:
π log(x) = x log(π)
Next, let C = -log(π)/π. Then, exponentiating gives
x = exp( -C x )
or
x exp(C x) = 1.
Finally, multiply both sides by C and define w = C*x to obtain the equation w*exp(w) = C.
The exact solution to the equation is w*exp(w) = C is w=W(C), where W is Lambert's W function. Furthermore, if -1/e < C < 0 then there are two branches to the Lambert W function, with corresponding solutions w1 and w2. Transforming back to the x scale, the roots are x1 = w1 / C and x2 = w2 / C.
In SAS, you can use the LAMBERTW function in PROC IML to obtain a direct solution to the equation f(x) - g(x) = 0, as follows.
/* The equation x^pi = pi^x has the exact solution x = LambertW(C) / C where C = -log(pi) / pi. Because C is slightly negative, there are two solutions. */ proc iml; pi = constant('pi'); c = -log(pi)/pi; w1 = LambertW(c); /* solve the Lambert equation for the main branch */ x1 = w1 / c; /* convert back to x scale */ print x1; isTwoRoots = (-1/exp(1) < c) & (c < 0); /* is there a second solution? */ if isTwoRoots then do; w2 = LambertW(c, -1); /* solve the Lambert equation for the second branch */ x2 = w2 / c; print x2; end; QUIT; |
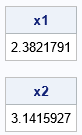
The program uses the Lambert W function to find the two numerical solutions to the equation xπ = πx. One of the solutions is obviously π. That there is a second solution (2.382179...) might be surprising to some people. For more information, see "Use the Lambert W function to solve equations that involve exponential functions."
The super-exponential function
There is another function that relates to the number ππ. It is the super-exponential function h(x) = xx. I call this function "super-exponential" because it increases faster than any exponential function. Obviously, ππ is the value of the function at evaluated at x=π. The super-exponential function is not as well-known as the class of power functions or exponential functions, but it is a standard example in calculus because its derivative is found by using implicit differentiation. For the record, the derivative is h'(x) = xx * (ln(x) + 1), which increases more rapidly than f does!
If I ask you to find the value of x for which h(x) = C, where C is a large constant, you could use a generic root-finding method (such as the FROOT function in SAS IML). However, the values of the super-exponential function are large for even moderately large values of x. Raising a large number to a large power can lead to numerical overflow or inaccuracies. Consequently, a better numerical method is to log-transform the equation and instead find the roots of log(h(x)) - log(C) = x*log(x) - log(C). The value of x that solves this log-transformed equation is also a solution to the original equation. However, the log-transformed equation is less likely to overflow and can be solved for much larger values of x.
This trick is ubiquitous in computational mathematics. For example, statisticians always use a log-likelihood instead of the likelihood function when they want to obtain maximum likelihood estimates.
Summary
Pi Day is a chance to celebrate the number π and to learn a little math. This article was motivated by a post on social media that tried to fool the reader into thinking that the number ππ is incredibly complicated to define. No, it is not any more complicated than 22 or 33, but you will need a calculator to find that ππ ≈ 36.462159607....
Not surprisingly, the number ππ is also a solution to the nonlinear equation πx = xπ. However, if you look more carefully at that equation, you discover that there is a second solution. You can express the second solution in terms of the Lambert W function, which is a tool in numerical analysis that you can use to obtain a direct solution to some equations that involve exponential functions. You can use the LAMBERTW function in SAS IML software to find the second solution is 2.3821791....
Lastly, the number ππ is the result of evaluating the function xx at x=π. It is worthwhile to remember that you can log-transform equations that involve positive quantities. The log-transformed equations are often better conditioned and easier to solve numerically.

1 Comment
Interesting coincidence: 10(pi^pi) - 1.5(pi) ~= degrees in a circle. Fun