One of my friends likes to remind me that "there is no such thing as a free lunch," which he abbreviates by "TINSTAAFL" (or TANSTAAFL). The TINSTAAFL principle applies to computer programming because you often end up paying a cost (in performance) when you call a convenience function that simplifies your program.

I was thinking about TINSTAAFL recently when I was calling a Base SAS function from the SAS/IML matrix language. The SAS/IML language supports hundreds of built-in functions that operate on vectors and matrices. However, you can also call hundreds of functions in Base SAS and pass in vectors for the parameters. It is awesome and convenient to be able to call the virtual smorgasbord of functions in Base SAS, such as probability function, string matching functions, trig function, financial functions, and more. Of course, there is no such thing as a free lunch, so I wondered about the overhead costs associated with calling a Base SAS function from SAS/IML. Base SAS functions typically are designed to operate on scalar values, so the IML language has to call the underlying function many times, once for each value of the parameter vector. It is more expensive to call a function a million times (each time passing in a scalar parameter) than it is to call a function one time and pass in a vector that contains a million parameters.

To determine the overhead costs, I decided to test the cost of calling the MISSING function in Base SAS. The IML language has a built-in syntax (b = (X=.)) for creating a binary variable that indicates which elements of a vector are missing. The call to the MISSING function (b = missing(X)) is equivalent, but requires calling a Base SAS many times, once for each element of x. The native SAS/IML syntax will be faster than calling a Base SAS function (TINSTAAFL!), but how much faster?

The following program incorporates many of my tips for measuring the performance of a SAS computation. The test is run on large vectors of various sizes. Each computation (which is very fast, even on large vectors) is repeated 50 times. The results are presented in a graph. The following program measures the performance for a character vector that contains all missing values.

/* Compare performance of IML syntax
   b = (X = " ");
   to performance of calling Base SAS MISSING function 
   b = missing(X);
*/
proc iml;
numRep = 50;                            /* repeat each computation 50 times */
sizes = {1E4, 2.5E4, 5E4, 10E4, 20E4};  /* number of elements in vector */
labl = {"Size" "T_IML" "T_Missing"};
Results = j(nrow(sizes), 3);
Results[,1] = sizes;
 
/* measure performance for character data */
do i = 1 to nrow(sizes);
   A = j(sizes[i], 1, " ");            /* every element is missing */
   t0 = time();
   do k = 1 to numRep;
      b = (A = " ");                   /* use built-in IML syntax */
   end;
   Results[i, 2] = (time() - t0) / numRep;
 
   t0 = time();
   do k = 1 to numRep;
      b = missing(A);                  /* call Base SAS function */
   end;
   Results[i, 3] = (time() - t0) / numRep;
end;
 
title "Timing Results for (X=' ') vs missing(X) in SAS/IML";
title2 "Character Data";
long = (sizes // sizes) || (Results[,2] // Results[,3]);   /* convert from wide to long for graphing */
Group = j(nrow(sizes), 1, "T_IML") // j(nrow(sizes), 1, "T_Missing"); 
call series(long[,1], long[,2]) group=Group grid={x y} label={"Size" "Time (s)"} 
            option="markers curvelabel" other="format X comma8.;";

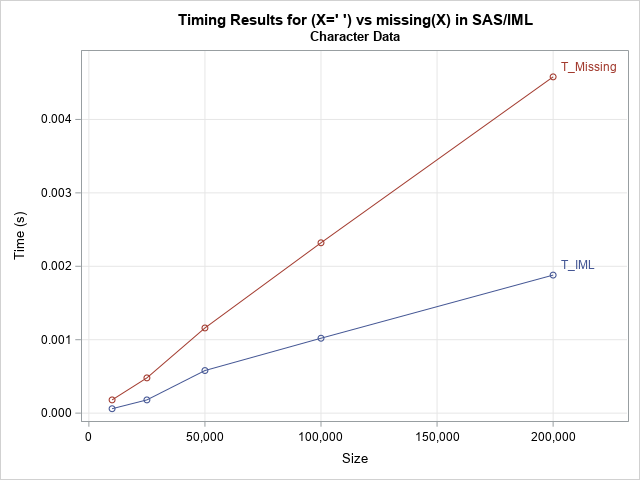
The graph shows that the absolute times for creating a binary indicator variable is very fast for both methods. Even for 200,000 observations, creating a binary indicator variable takes less than five milliseconds. However, on a relative scale, the built-in SAS/IML syntax is more than twice as fast as calling the Base SAS MISSING function.

You can run a similar test for numeric values. For numeric values, the SAS/IML syntax is about 10-20 times faster than the call to the MISSING function, but, again, the absolute times are less than five milliseconds.

So, what's the cost of calling a Base SAS function from SAS/IML? It's not free, but it's very cheap in absolute terms! Of course, the cost depends on the number of elements that you are sending to the Base SAS function. However, in general, there is hardly any cost associated with calling a Base SAS function from SAS/IML. So enjoy the lunch buffet! Not only is it convenient and plentiful, but it's also very cheap!