SAS/STAT software contains a number of so-called HP procedures for training and evaluating predictive models. ("HP" stands for "high performance.") A popular HP procedure is HPLOGISTIC, which enables you to fit logistic models on Big Data. A goal of the HP procedures is to fit models quickly. Inferential statistics such as standard errors, hypothesis tests, and p-values are less important for Big Data because, if the sample is big enough, all effects are significant and all hypothesis tests are rejected! Accordingly, many of the HP procedures do not support the same statistical tests as their non-HP cousins (for example, PROC LOGISTIC).
A SAS programmer recently posted an interesting question on the SAS Support Community. She is using PROC HPLOGISTIC for variable selection on a large data set. She obtained a final model, but she also wanted to estimate the covariance matrix for the parameters. PROC HPLOGISTIC does not support that statistic but PROC LOGISTIC does (the COVB option on the MODEL statement). She asks whether it is possible to get the covariance matrix for the final model from PROC LOGISTIC, seeing as PROC HPLOGISTIC has already fit the model? Furthermore, PROC LOGISTIC supports computing and graphing odds ratios, so is it possible to get those statistics, too?
It is an intriguing question. The answer is "yes," although PROC LOGISTIC still has to perform some work. The main idea is that you can tell PROC LOGISTIC to use the parameter estimates found by PROC HPLOGISTIC.
What portion of a logistic regression takes the most time?
The main computational burden in logistic regression is threefold:
- Reading the data and levelizing the CLASS variables in order to form a design matrix. This is done once.
- Forming the sum of squares and crossproducts matrix (SSCP, also called the X`X matrix). This is done once.
- Maximizing the likelihood function. The parameter estimates require running a nonlinear optimization. During the optimization, you need to evaluate the likelihood function, its gradient, and its Hessian many times. This is an expensive operation, and it must be done for each iteration of the optimization method.
The amount of time spent required by each step depends on the number of observations, the number of effects in the model, the number of levels in the classification variables, and the number of computational threads available on your system. You can use the Timing table in the PROC HPLOGISTIC output to determine how much time is spent during each step for your data/model combination. For example, the following results are for a simulated data set that has 500,000 observations, 30 continuous variables, four CLASS variables (each with 3 levels), and a main-effects model. It is running on a desktop PC with four cores. The iteration history is not shown, but this model converged in six iterations, which is relatively fast.
ods select PerformanceInfo IterHistory Timing; proc hplogistic data=simLogi OUTEST; class c1-c&numClass; model y(event='1') = x1-x&numCont c1-c&numClass; ods output ParameterEstimates=PE; performance details; run; |
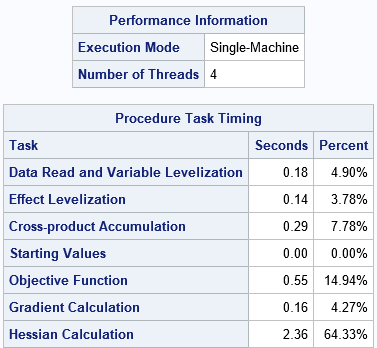
For these data and model, the Timing table tells you that the HPLOGISITC procedure fit the model in 3.68 seconds. Of that time, about 17% was spent reading the data, levelizing the CLASS variables, and accumulating the SSCP matrix. The bulk of the time was spent evaluating the loglikelihood function and its derivatives during the six iterations of the optimization process.
Reduce time in an optimization by improving the initial guess
If you want to improve the performance of the model fitting, about the only thing you can control is the number of iterations required to fit the model. Both HPLOGISTIC and PROC LOGISTIC support an INEST= option that enables you to provide an initial guess for the parameter estimates. If the guess is close to the final estimates, the optimization method will require fewer iterations to converge.
Here's the key idea: If you provide the parameter estimates from a previous run, then you don't need to run the optimization algorithm at all! You still need to read the data, form the SSCP matrix, and evaluate the loglikelihood function at the (final) parameter estimates. But you don't need any iterations of the optimization method because you know that the estimates are optimal.
How much time can you save by using this trick? Let's find out. Notice that the previous call used the ODS OUTPUT statement to output the final parameter estimates. (It also used the OUTEST option to add the ParmName variable to the output.) You can run PROC TRANSPOSE to convert the ParameterEstimates table into a data set that can be read by the INEST= option on PROC HPLOGISTIC or PROC LOGISTIC. For either procedure, set the option MAXITER=0 to bypass the optimization process, as follows:
/* create INEST= data set from ParameterEstimates */ proc transpose data=PE out=inest(type=EST) label=_TYPE_; label Estimate=PARMS; var Estimate; id ParmName; run; ods select PerformanceInfo IterHistory Timing; proc hplogistic data=simLogi INEST=inest MAXITER=0; class c1-c&numClass; model y(event='1') = x1-x&numCont c1-c&numClass; performance details; run; |
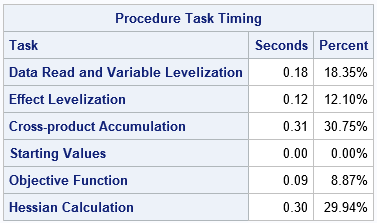 The time required to read the data, levelize, and form the SSCP is unchanged. However, the time spent evaluating the loglikelihood and its derivatives is about 1/(1+NumIters) of the time from the first run, where NumIters is the number of optimization iterations (6, for these data). The second call to the HPLOGISTIC procedure still has to fit the loglikelihood function to form statistics like the AIC and BIC. It needs to evaluate the Hessian to compute standard errors of the estimates. But the total time is greatly decreased by skipping the optimization step.
The time required to read the data, levelize, and form the SSCP is unchanged. However, the time spent evaluating the loglikelihood and its derivatives is about 1/(1+NumIters) of the time from the first run, where NumIters is the number of optimization iterations (6, for these data). The second call to the HPLOGISTIC procedure still has to fit the loglikelihood function to form statistics like the AIC and BIC. It needs to evaluate the Hessian to compute standard errors of the estimates. But the total time is greatly decreased by skipping the optimization step.
Use PROC HPLOGISTIC estimates to jump-start PROC LOGISTIC
You can use the same trick with PROC LOGISTIC. You can use the INEST= and MAXITER=0 options to greatly reduce the total time for the procedure. At the same time, you can request statistics such as COVB and ODDSRATIO that are not available in PROC HPLOGISTIC, as shown in the following example:
proc logistic data=simLogi INEST=inest plots(only MAXPOINTS=NONE)=oddsratio(range=clip); class c1-c&numClass; model y(event='1') = x1-x&numCont c1-c&numClass / MAXITER=0 COVB; oddsratio c1; run; |
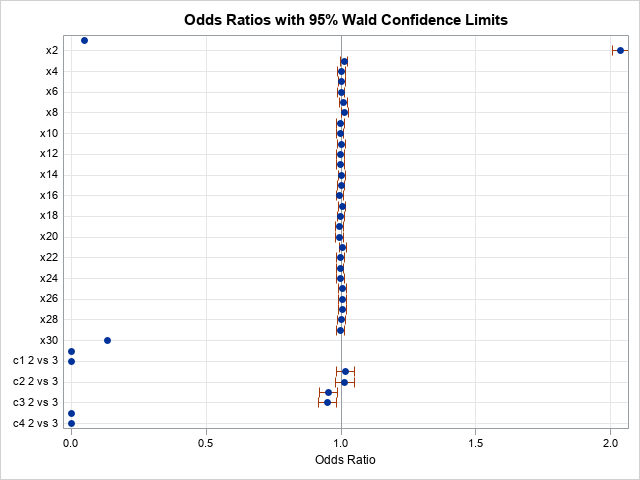
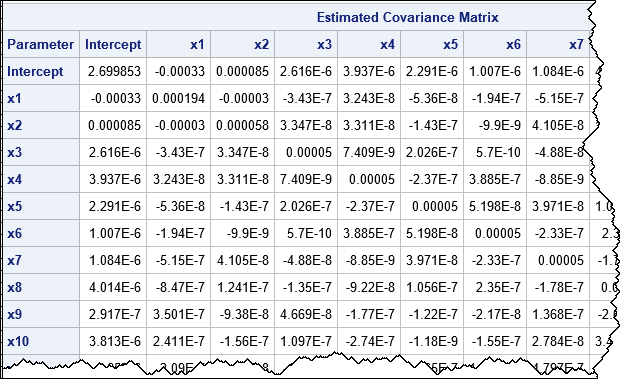
The PROC LOGISTIC step takes about 4.5 seconds. It produces odds ratios and plots for the model effects and displays the covariance matrix of the betas (COVB). By using the parameter estimates that were obtained by PROC HPLOGISTIC, it was able to avoid the expensive optimization iterations.
You can also use the STORE statement in PROC LOGISTIC to save the model to an item store. You can then use PROC PLM to create additional graphs and to run additional post-fit analyses.
In summary, PROC LOGISTIC can compute statistics and hypothesis tests that are not available in PROC HPLOGISTIC. it is possible to fit a model by using PROC HPLOGISTIC and then use the INEST= and MAXITER=0 options to pass the parameter estimates to PROC LOGISTIC. This enables PROC LOGISTIC to skip the optimization iterations, which saves substantial computational time.
You can download the SAS program that creates the tables and graphs in this article. The program contains a DATA step that simulates logistic data of any size.

1 Comment
Pingback: How to score a logistic regression model that was not fit by PROC LOGISTIC - The DO Loop