To a statistician, the LAG function (which was introduced in SAS/IML 9.22) is useful for time series analysis. To a numerical analyst and a statistical programmer, the function provides a convenient way to compute quantitites that involve adjacent values in any vector.

The LAG function is essentially a "shift operator." It shifts a vector of values and pads the result with missing values so that the returned vector has the same number of elements as the original vector. For example, the following SAS/IML statements define the first few terms of the Fibonacci series and call the LAG function to shift the series by one element.

proc iml;
v = {1, 1, 2, 3, 5, 8, 13, 21}; /* Fibonacci sequence */
lag1 = lag(v);            /* by default, lag=1 ==> shift forward */
first = 1:(nrow(v)-1);    /* index 1:(N-1) */
v1 = v[first];            /* extract all but the last element */
print lag1 v1;

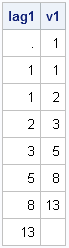
The returned vector, lag1, contains a missing value in the first element and does not contains the last element of v. Notice that the nonmissing values are similar to v1, which is obtained by subsetting the first N-1 elements of the vector v.

You can shift elements the other way by using a negative value for the lag parameter. (This is sometimes called computing a lead.)

lag2 = lag(v, -1);       /* shift backward */
last = 2:nrow(v);        /* index 2:N */
v2 = v[last];            /* extract all but first element */

The returned vector (not shown) contains a missing value in the last element and does not contains the first element of v.

The LAG function is valuable when you want to compute a quantity that involves adjacent elements. For example, the following statements compute the ratio of adjacent values in the Fibonacci sequence:

z = v/lag(v); /* ratio of adjacent values */
print z;

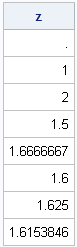
This ratio quickly converges to the Golden Ratio, which is which is 1.61803399.... In a previous post, I show how you can undestand this result by looking at the eigenvalues of a certain linear transformation.

So, yes, by all means, use the LAG function to compute lags and leads in time series data. However, the LAG functon is also useful for any numerical computation that involves adjacent values in a sequence.