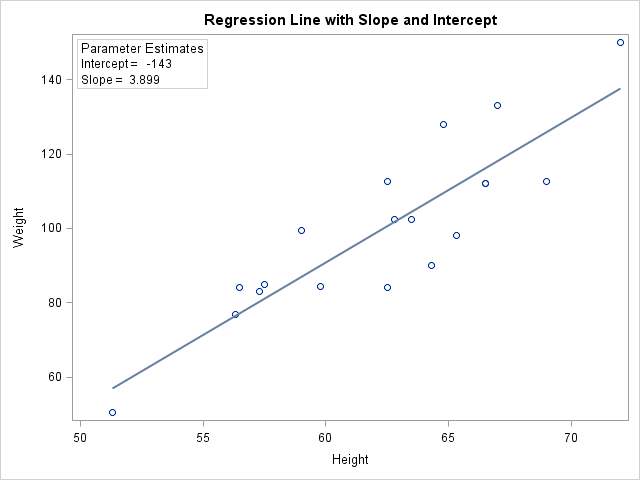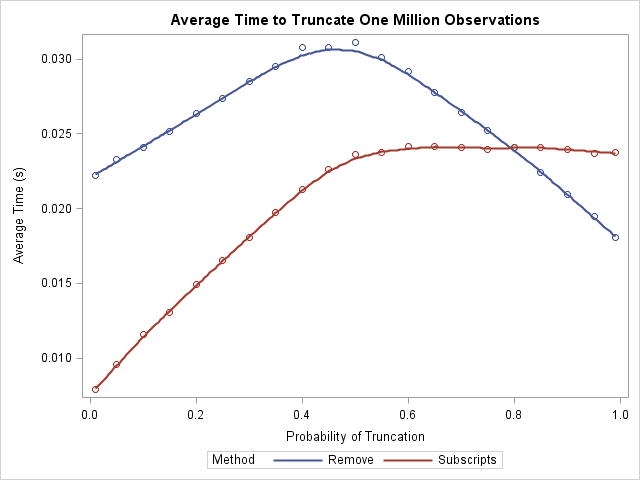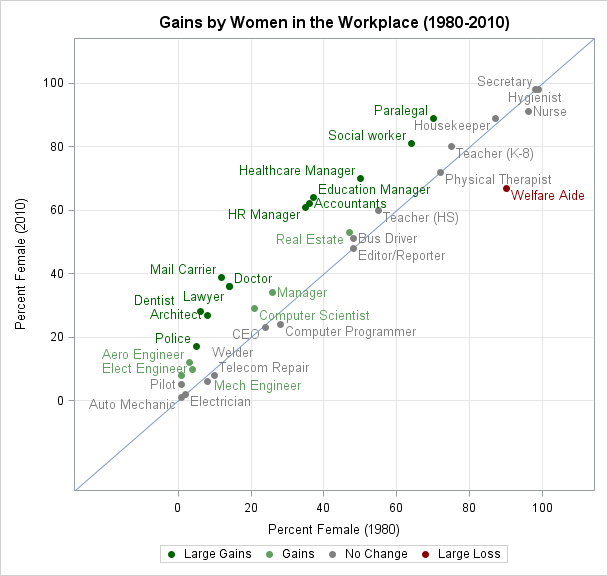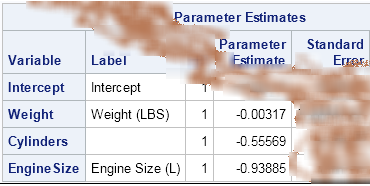
Argh! I've just spilled coffee on output that shows the least squares coefficients for a regression model that I was investigating. Now the parameter estimate for the intercept is completely obscured, although I can still see the parameter estimates for the coefficients of the continuous explanatory variable. What can I