Permute the order of rows in a matrix

In some applications, it is useful to permute the rows or the columns of a matrix. A previous article discusses how random permutation of columns (within each row) are useful in constructing permutation tests. This article shows a simpler situation: Permuting the rows of a matrix to change their order. One application is to sort the rows according to a statistic, but there are other applications, too.

Let's start with an example matrix that has seven rows. To make the permutations easier to see, the first element in each row is the row number:

proc iml;
M = {
1  2  3  4  5 ,
2  7  8  9 10 ,
3 12 13 14 15 ,
4 17 18 19 20 ,
5 22 23 24 25 ,
6 27 28 29 30 ,
7 32 33 34 35 
};
nc = ncol(M);      /* nr = number of rows */
nr = nrow(M);      /* nc = number of columns */

Random permutations of rows

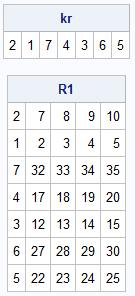
Some applications require a random permutation of the rows. In the SAS IML language, the RANPERM function returns a random permutation of the set {1,2,3,...,n}. If you generate a random permutation, you can use it as the row indices in a subscript operation to obtain a permuted matrix, as follows:

/* random permutation of rows */
call randseed(12345);
kr = ranperm(nr);     /* random permutation of {1,2,3,..., nr} */
R1 = M[kr, ];
print kr, R1;

Cyclic permutation of rows

A special kind of permutation is called a cyclic permutation. In a cyclic permutation, all values are shifted to the right by some number of positions. Those values that "fall off the end" are wrapped around and appear in the leftmost positions. For example, a cyclic permutation that shifts the values in the vector v={1,2,3,4,5} by two positions is the vector w={4,5,1,2,3}.

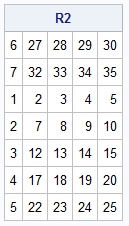
For computer languages that use 0-based indexing, it is easy to program a cyclic permutation by using the MOD operator. If d is the length of a vector, v, and you want to shift the elements to the right by s positions, then the new vector, w, is defined by w[mod(i+s, d)] = v[i], i=0,1,...,d-1. Again, this assumes 0-based indexing. Equivalently, you can write the transformation as w[i]= v[mod(i-s, d)] if the MOD function always returns positive values. Unfortunately, the MOD function in SAS might return a negative value, so you must add d to the formula to ensure proper indexing: w[i]= v[mod(i+d-s, d)]. Lastly, indexing in the IML language is 1-based, not 0-based, so you need to subtract 1 before applying the MOD function and then add 1 to the result. The following statements show how to generate a cyclic permutation and use it to shift the rows of a matrix:

/* shift indices 1:d by k (mod d).
   For example, if d=5 and k=2, v=1:5 shifted by 2 (mod 5) is {4 5 1 2 3} */
start CyclicShift(k, d);
   idx = (1:d) + (d - k);          /* assume k < d */
   shiftIdx = mod(idx-1, d) + 1;   /* for 1-based indices: subtract 1 before applying MOD, then add it back */
   return shiftIdx;
finish;
 
k = 2;
newIdx = CyclicShift(k, nrow(M));
R2 = M[newidx, ];
print R2;

Perform cyclic or specific permutation of rows

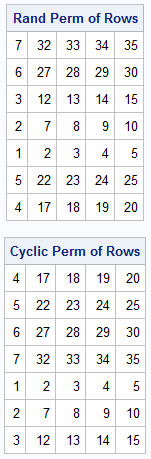
You can combine the ideas in the previous two sections. The following program contains a SAS IML function that takes two arguments. The first is the matrix, M, whose rows you want to permute. The second argument specifies the permutation. If the second argument, k, is a scalar, you can treat is as the cyclic permutation i → i+k (mod d), where d is the number of rows in M. Otherwise, assume that k is a vector that is a permutation of 1:d and apply that permutation. The program shows two examples of calling the function. The first call uses a vector for the second argument; the second call passes in a scalar, which indicates a cyclic permutation:

/* M is a matrix with d rows. 
   If k is a scalar 1 <= k < d, perform a cyclic permutation of rows of M by shifting rows by k positions
   If k is a vector that has d elements, use k as the indices for the permutation
*/
start PermuteRows(M, _k);
   k = colvec(_k);
   if nrow(k)=nrow(M) then 
      R = M[k, ];      /* user-specified permutation */
   else if nrow(k)=1 then do;
      newIdx = CyclicShift(k, nrow(M));
      R = M[newidx, ]; /* cyclic permutation */
      end;
   else 
      STOP "ERROR: In PermuteRows, k must be a scalar or nrow(k)=nrow(M)";
   return R;
finish;
 
k = {7,6,3,2,1,5,4};
R1 = PermuteRows(M, k);     /* permute according to k */
R2 = PermuteRows(M, 4);     /* cyclic permutation: shift rows by 4 */
print R1[L='Rand Perm of Rows'], R2[L='Cyclic Perm of Rows'];

Summary

This article shows how to permute the rows of a matrix by specifying a permutation vector. In addition, it shows how to create a permutation vector for a cyclic permutation where each row moves down by k positions and the last k rows get moved to the top.

Blogs