Convert integers between different bases in SAS

While many applications of Monte Carlo techniques use pseudorandom numbers, some applications that involve integrals are more accurate when you use quasirandom numbers, which, despite their names, are not random but are deterministic sequences of numbers. Many of these sequences are constructed by representing base-10 numbers in a different base. Familiar bases include b=2 (binary), b=3 (ternary), and b=16 (hexadecimal). The following tasks are important when converting numbers to and from bases:

Compute how many digits a base 10 number has when represented in an arbitrary base. This requires computing logarithms in an arbitrary base.
Convert a number from base 10 to an arbitrary base.
Convert a number from an arbitrary base to base 10.

This article shows how to compute these quantities by using the SAS IML language. I have previously presented DATA step implementations for a few of these tasks. However, since my ultimate goal is to perform quasi-Monte Carlo computations, the SAS IML language is a better choice.

The logarithm (base b) of a number

In working with arbitrary bases, it is useful to be able to evaluate the logarithm function, x = log_b(n). Many computer languages, including SAS, support built-in functions only for log₁₀ (LOG10), log₂ (LOG2), and the natural logarithm log_e (LOG).

To compute the logarithm for an arbitrary base, b, you can use the "change-of-base formula,"
$\log_b(n) = \log_k(n) / \log_k(b)$
where k can be any convenient base. For details, see a previous article on this topic.

Because computers natively operate in binary, choosing k=2 makes the computation more efficient. The following SAS IML function implements the formula for any base, b. You can pass in a vector of x values as the input. If any element is not positive, the function returns a missing value for that element.

proc iml;
/* Compute LOG_b(x) for a vector of x values and for an integer base, b > 0.
   If an input value is not positive, this function returns a missing value.
*/
start logbase(x, base=10);
   if all(x)>0 then 
      return log2(x) / log2(base);
   /* otherwise, return missing values for x <= 0 */
   y = j(nrow(x), ncol(x), .);
   idx = loc(x>0);
   if ncol(idx)>0 then 
      y[idx] = log2(x[idx]) / log2(base);
   return y;
finish;
 
/* test the function for base b=2 and 3 */
t = {2,3,4,5,8,9,15,16,48};
log2 = logbase(t, 2);
log3 = logbase(t, 3);
print t log2 log3;

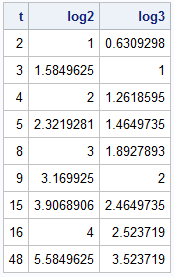
The number of digits in a base-b representation of an integer

You can use the base-b logarithm to compute the number of digits required to represent an integer n in an arbitrary base b. As explained in a previous article, the number of digits, k, is given by the formula
k = ceil(log_b(n+1))

The following function calls the logbase function in the previous section:

/* This function returns the number of digits in the base-b representation of an integer, x.
   If n >= 0 is a base-10 integer, it has
      k = ceil(log_b(n+1))
   digits when represented in base b. See
   https://blogs.sas.com/content/iml/2015/08/31/digits-in-integer.html
*/
start numDigBase(x, base=10);
   n = round(x);              /* ensure argument is an integer */
   return ceil( logbase(n+1,base) );
finish;
 
/* test the function for base b=2 and 3 */
t = {2,3,4,5,8,9,15,16,48};
numDig2 = numDigBase(t, 2);
numDig3 = numDigBase(t, 3);
print t numDig2 numDig3;

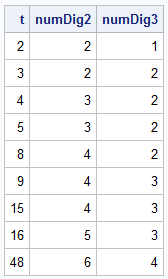
Convert an integer from base 10 to another base

I previously wrote an article that explains how to convert an integer from base 10 to another base. The technique uses repeated division: you divide n by the base b, store the remainder as the next digit, and continue the division until the quotient is zero. You can use the MOD and FLOOR functions to perform these operations.

For example, if you want to convert 15 (base 10) to base 3:

15 / 3 = 5 remainder 0, so store 0 as the least significant bit and use 5 as the next value of 'n'. The least significant bit is the rightmost digit.
5 / 3 = 1 remainder 2, so store 2 as the next digit and use 1 as the next value of 'n'.
1 / 3 = 0 remainder 1, so store 1 as the next digit. The method ends.

Thus, 15 (base 10) = 120 (base 3). The previous article includes a DATA step that implements the technique. But you can vectorize the computation in PROC IML to make it more efficient. The following function accepts a vector of inputs, which are positive base-10 integers. It returns a matrix of digits where the i_th row represents the i_th integer in the specified base. The number of rows in the matrix is determined by using the numDigBase function on the largest input value.

/* Convert integer x > 0 to a row vector in base b.
   If x is a column vector, return a matrix where each row is the base-b representation of x[i].
   The most significant bit is to the left; the least significant bit is to the right.
   For example, n=15 and base=3 gives (120)_3 because 15 = 1*3##2 + 2*3##1 + 0*3##0.
*/
start convertToBase(x, base);
   n = round(x);     /* ensure inputs are integers */
   numDig = numDigBase(max(n), base);
   /* For an explanation, see https://blogs.sas.com/content/iml/2015/08/31/digits-in-integer.html */
   c = j(nrow(n), numDig, 0);
   do i = 1 to numDig;
      a = mod(n, base);
      n = floor( n/base );
      c[ , numDig - i + 1] = a;
   end;
   return c;
finish;
 
/* test the function for base b=2 and 3 */
t = {2,3,4,5,8,9,15,16,48};
base2 = ConvertToBase(t, 2);
base3 = ConvertToBase(t, 3);
print base2[r=t c=('c5':'c0')];
print base3[r=t c=('c3':'c0')];

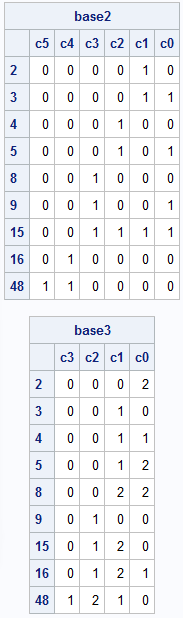
Convert to base 10 from an arbitrary base

I have previously shown how to convert a number from base 2 to base 10. The process is similar for other bases. The input is a row vector of digits (0 through b-1) in the specified base. The output is a base-10 integer. You can vectorize the computations so that the input can be a matrix of digits, where each row is a base-b representation of an integer. Then the output is a vector of integers.

/* Convert a row vector from any base to a number in base 10.
   If c is a kxm matrix, then return a base-10 number fo each row.
   For example, in base 3, define:
   c = {0 1 2 1,   
        1 2 1 0 };
   The first row represents 16. The second row represents 48.
   See https://blogs.sas.com/content/iml/2011/11/16/converting-from-base-2-to-base-10.html 
*/
start ConvertFromBase(c, base);
   pow = (ncol(c)-1):0;
   factor = base##pow;
   base10 = (c # factor)[ ,+];  /* c[k-1]*b##(k-1) + ... + c[1]*b##1 + c[0]*b##0 */ 
   return base10;
finish;
 
/* test the function for base b=2 and 3 */
n2 = ConvertFromBase(base2, 2);
n3 = ConvertFromBase(base3, 3);
print n2 n3;

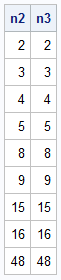
Summary

This article introduces four SAS IML functions that are useful for converting an integer, n, between base 10 and an arbitrary base, b. The first enables you to compute the logarithm of n in base b. The others enable you to count the number of digits required to represent n in base b, to convert n from base 10 into base b, and to convert a number in base b to base 10. Examples are given for b=2 and b=3. In quasirandom Monte Carlo applications, the base is often a prime number. These functions are useful for working with integer sequences in arbitrary bases. In a future article, I show how to use these functions to generate quasirandom numbers.

Blogs