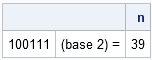
Here is a little trick to file away. Given a row vector of zeros and ones, thought of as representing a number in base 2, the following SAS/IML statements compute the decimal value of that vector.

proc iml;
x = {1 0 0 1 1 1}; /* number in base 2 */
pow = (ncol(x)-1):0; /* exponents */
placeVals = 2##pow; /* base raised to exponent power */
n = sum(placeVals # x);
print (rowcatc(char(x))) "(base 2) =" n;

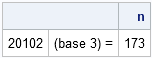
The astute observer will notice that the same idea can be used to convert a number in any base to its base 10 equivalent. Here is a general-purpose module:

/* convert a number from base b to base 10 */
start ConvertFromBase(x, b);
   if any(x>=b) then abort; /* invalid number */
   pow = (ncol(x)-1):0; /* exponents */
   placeVals = b##pow; /* base raised to exponent power */
   return( sum(placeVals # x) );
finish;
 
/* call the module */
y = {2 0 1 0 2}; /* number in base 3 */
n = ConvertFromBase(y, 3);
print (rowcatc(char(y))) "(base 3) =" n;

Interestingly, there is another approach that converts a string of zeros and ones to a binary value. All you need to do is apply the BINARY. format to the value, as shown in the following statements:

s = "100111";
val = inputn(s, "Binary.");

Non-decimal bases don't arise in statistical programming very often. However, they arise often enough that it's worth squirreling this trick away until it is needed.