Many people know that a surface can contain a saddle point, but did you know that you can define the saddle point of a matrix? Saddle points in matrices are somewhat rare, which means that if you choose a random matrix you are unlikely to choose one that has a saddle point. This article shows how to
- Locate a saddle point in a matrix
- Use simulation to estimate the probability of finding a saddle point in a random matrix.
- Use simulation to explore the distribution of the location of a saddle point in a random matrix.
A saddle point of a matrix
You might remember from multivariable calculus that a critical point (x0, y0) is a saddle point of a function f if it is a local minimum of the surface in one direction and a local maximum in another direction. The canonical example is f(x,y) = x2 - y2 at the point (x0, y0) = (0, 0). Along the horizontal line y=0, the point (0, 0) is a local minimum. Along the vertical line x=0, the point (0, 0) is a local maximum.
The definition of a saddle point of a matrix is similar. For an n x p matrix M, the cell (i, j) is a saddle point of the matrix if M[i, j] is simultaneously the minimum value of the i_th row and the maximum value of the j_th column.
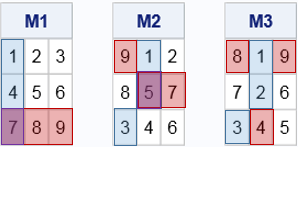
Consider the following 3 x 3 matrices. The minimum value for each row is highlighted in blue. The maximum value for each column is highlighted in red. Two of the matrices have saddle points, which are highlighted in purple.
- For the matrix M1, the (3, 1) cell is a saddle point because 7 is the smallest value in row 3 and the largest value in column 1.
- For the matrix M2, the (2, 2) cell is a saddle point because 5 is the smallest value in row 2 and the largest value in column 2.
- The matrix M3 does not have a saddle point. No cell is simultaneously the smallest value in its row and the largest value in its column.
Compute the location of a saddle point in a matrix
In a matrix language such as SAS/IML, you can use row and column operators to find the location of a saddle point, if it exists. The SAS/IML language supports subscript reduction operators, which enable you to compute certain statistics for all rows or all columns without writing a loop. For this problem, you can use the "index of the minimum operator" (>:<) to find the elements that are the minimum for each row and the "index of the maximum operator" (<:>) to find the elements that are the maximum for each column. To find whether there is an element in common, you can use the XSECT function find the intersection of the two sets. (SAS/IML supports several functions that perform set operations.)
A function that computes the location of the saddle point follows. It uses the SUB2NDX function to convert subscripts to indices.
proc iml; start LocSaddlePt(M); dim = dimension(M); n = dim[1]; p = dim[2]; minRow = M[ ,>:<]; /* for each row, find column that contains min */ minSubscripts = T(1:n) || minRow; /* location as (i,j) pair */ minIdx = sub2ndx(dim, minSubscripts); /* convert location to index in [1, np] */ maxCol = T(M[<:>, ]); /* for each column, find row that contains max */ maxSubscripts = maxCol || T(1:p); /* loation as (i,j) pair */ maxIdx = sub2ndx(dim, maxSubscripts); /* convert location to to index in [1, np] */ xsect = xsect(minIdx, maxIdx); /* intersection; might be empty matrix */ if ncol(xsect) > 0 then return ( xsect ); else return ( . ); finish; M1 = {1 2 3, 4 5 6, 7 8 9}; idx1 = LocSaddlePt(M1); M2 = {9 1 2, 8 5 7, 3 4 6}; idx2 = LocSaddlePt(M2); M3 = {8 1 9, 7 2 6, 3 4 5}; idx3 = LocSaddlePt(M3); print idx1 idx2 idx3; |
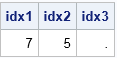
The indices of the saddle points are shown for the three example matrices. The 7th element of the M1 matrix is a saddle point, which corresponds to the (3, 1) cell for a 3 x 3 matrix in row-major order. The 5th element (cell (2,2)) of the M2 matrix is a saddle point. The M3 matrix does not contain a saddle point.
The probability of a saddle point in a 3x3 random matrix
A matrix contains either zero or one saddle point. There is a theorem (Ord, 1979) that says that the probability of finding a saddle point in a random n x p matrix is (n! p!) / (n+p-1)! when the elements of the matrix are randomly chosen from any continuous probability distribution.
Although the theorem holds for any continuous probability distribution, it suffices to prove it for the uniform distribution. Notice that the existence and location of a saddle point is invariant under any monotonic transformation because those transformations do not change the relative order of elements. In particular, if F is any probability distribution, the existence and location of the saddle point is invariant under the monotonic transformation F–1, which transforms the numbers into a sample from the uniform distribution. In fact, you can replace the number by their ranks, which converts the random matrix into a matrix of that contains the consecutive integers 1, 2, ..., np. Thus the previous integer matrices represent the ranks of a random matrix where the elements are drawn from any continuous distribution.
For small values of n and p, you can use the ALLPERM function to enumerate all possible matrices that have integers in the range [1, np]. You can reshape the permutation into an n x p matrix and compute whether the matrix contains a saddle point. If you use a 0/1 indicator array to encode the result, then the exact probability of finding a saddle point in a random n x p matrix is found by computing the mean of the indicator array. The following example computes the exact probability of finding a saddle point in a random 3 x 3 matrix:
A = allperm(9); /* all permutations of 1:9 */ saddle = j(nrow(A), 1); /* allocate vector for results */ do i = 1 to nrow(A); /* for each permutation (row) ... */ M = shape(A[i,], 3); /* reshape row into 3x3 matrix */ idx = LocSaddlePt( M ); /* find location of saddle */ saddle[i] = (idx > 0); /* 0/1 indicator variable */ end; prob = saddle[:]; /* (sum of 1s) / (number of matrices) */ print prob; |
As you can see, the computational enumeration shows that the probability of a saddle point is 0.3 for 3 x 3 matrices. This agrees with the theoretical formula (3! 3!) / 5! = 36 / 120 = 3/10.
The probability of a saddle point in a random matrix
Of course, when n and p are larger it becomes infeasible to completely enumerate all n x p matrices. However, you can adopt a Monte Carlo approach: generate a large number of random matrices and compute the proportion which contains a saddle point. The following program simulates one million random 4 x 4 matrices from the uniform distribution and computes the proportion that has a saddle point. This is a Monte Carlo estimate of the true probability.
NSim = 1e6; n = 4; p=4; /* random 4x4 matrices from uniform distribution */ A = j(NSim, n*p); call randgen(A, "Uniform"); saddleLoc = j(NSim, 1, .); /* store location of the saddle point */ saddle = j(NSim, 1); /* binary indicator variable */ do i = 1 to NSim; /* Monte Carlo estimation of probability */ M = shape(A[i,], n, p); saddleLoc[i] = LocSaddlePt( M ); /* save the location 1-16 */ saddle[i] = (saddleLoc[i] > 0 ); /* 0/1 binary variable */ end; estProb = saddle[:]; Prob = fact(n)*fact(p) / fact(n+p-1); print estProb Prob; |
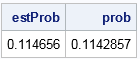
The output shows that the estimated probability agrees with the exact probability to four decimal places.
The distribution of locations of saddle points
The saddle point can occur in any cell in the matrix. Consider, for example, the integer matrix M1 from the earlier 3 x 3 example. If you swap the first and third rows of M1, you will obtain a new matrix that has a saddle point in the (1,1) cell. If you swap the second and third rows of M1, you obtain a saddle point in the (2,1) cell. Similarly, you can swap columns to move a saddle point to a different column. In general, you can move the saddle point to any cell in the matrix by a transposition of rows and columns. Thus each cell in the matrix has an equal probability of containing a saddle point, and the probability that the saddle point is in cell (i,j) is 1/(np) times to the probability that a saddle point exists.
In the preceding SAS/IML simulation, the saddleLoc variable contains the location of the saddle point in the 4 x 4 matrix. The following statements compute the empirical proportion of times that a saddle point appeared in each of the 16 cells of the matrix:
call tabulate(location, freq, saddleLoc); /* frequencies in cells 1-16 */ counts = shape(freq, n, p); /* shape into matrix */ EstProbLoc = counts / (NSim); /* empirical proportions */ print EstProbLoc[r=('1':'4') c=('1':'4') F=7.5]; |
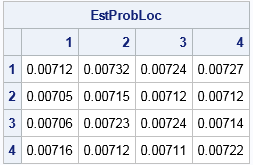
The output indicates that each cell has a probability that is estimated by 0.007 (the "James Bond" probability!). Theoretically, you can prove that the probability in each cell is given by the value of the complete beta function B(n, p), which for n=p=4 yields B(4,4) = 0.0071429 (Hofri, 2006).
In summary, this article has explored three topics that are dear to my heart: probability, simulation, and properties of matrices. Along the way, we encountered factorials, permutations, the complete beta function, and got to write some fun SAS/IML programs. For more information about the probability of a saddle point in random matrices, see "The probability that a matrix has a saddle point" (Thorp, 1979) and and "On the distribution of a saddle point value in a random matrix" (Hofri, 2006).

6 Comments
Can you comment on the mathematical significance of whether a matrix has a saddle point or not?
Mostly it is a curiosity. I don't think it is important to matrices in the same way that symmetry, positive definiteness, or eigenvalues are.
Saddle points are a particular arrangement among random values. Suppose A[1,1] is the saddle point, then it must be the case that A[1,1] < A[1,j] for each j and A[1,1] > A[i,1] for each i. The rarity of a saddle point is a way of saying that those n+p-2 inequalities are unlikely to happen when the values are selected at random from any distribution. In this way, a saddle point in a matrix can be thought of as a particular 2D arrangement within the set of all possible 2D arrangements. A 1D analogy would be investigating the probability of permutations such as [1 3 5 4 2] that increase monotonically until some value (5) and then decrease monotonically after that value. Is studying such an arrangement "mathematically significant"? Probably not, but it is interesting nontheless.
I understand saddle points in search algorithms a little via local minimums and maximums. We search for these points as solutions in some work. In that context would the saddle points not be very significant in some domains such as optimizations? Say we are optimizing something to be minimum in one dimension but maximum in some other dimension then finding the saddle points is finding our solution.
Now back to matrices. Are matrices not useful for mapping Markov chains? Now I am in the unknown for me a bit but speculating that some how saddle points would be useful in matrices representing Markov chains.
Yes, saddle points are important in optimization. A local extremum can be classified as a maximum, a minimum, or "something else", and a saddle point is an important sub-case of the "something else" category. For a continuous objective function, the first derivatives vanish at a local extremum and you use second derivatives to classify the type of extremum.
Regarding Markov transition matrices, if the cell (i,j) is a saddle point then it means that when the system is in "State i", it is least likely to transition to "State j" (minimum of row i). However, every other state has a higher probability of transitioning to "State j" (maximum of column j).
Thanks for sharing. Great suff!
Thanks!!! Gain is my favorite!