Last week I described how to generate permutations in SAS. A related concept is the "combination." In probability and statistics, a combination is a subset of k items chosen from a set that contains N items. Order does not matter, so although the ordered triplets (B, A, C) and (C, A, B) represent different permutations of three items, they are considered equivalent when regarded as sets. Consequently, a combination is usually presented in a canonical format, such as in alphanumeric order: {A, B, C}.
SAS/IML 9.3 introduced two functions for working with combinations: the ALLCOMB function, which enumerates all combinations, and the RANCOMB function, which generates random combinations.
Let's see how these functions could be used. I often eat salads for lunch. Suppose that each day I add three toppings to my lettuce, chosen from my five favorite items on the salad bar. If I want to create a schedule that rotates through all combinations of possible salad toppings, I could run the following SAS/IML program. The program uses the ALLCOMB function to enumerate the set of all combinations of five items chosen three at a time:
proc iml; N = 5; /* number of possible toppings */ k = 3; /* number of toppings per salad */ idx = allcomb(N, k); print idx; |

Each of the ten rows in the matrix is a combination of veggies. The first row corresponds to a salad with veggies 1, 2, and 3. To make it easier to read, I can name the five toppings and use these indices to extract the names:
Items = {"Broccoli" "Carrots" "Cucumbers" "Peppers" "Tomatoes"};
S = Items[ ,idx];
S = shape(S, 0, k); /* reshape S to have 3 cols */
print S[r=(char(1:nrow(S))) L="Salad Schedule"]; |
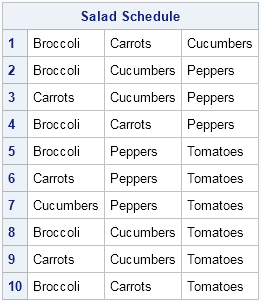
It will take me ten lunches to cycle through the distinct combinations of salad toppings. (Use the COMB function to compute "N choose k," which is the total number of combinations.) However, if I am feeling particularly daring—some would say a tad wild!—I could forego my orderly progression through the schedule and generate a random combination of veggies for my salad by using the RANCOMB function, as follows:
Toppings = rancomb(Items, 3); print Toppings[L="Today's Toppings"]; |
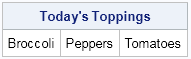
Although the salad example is intentionally whimsical, combinations are serious business in statistics, especially in the combinatorial design of experiments. In addition to the SAS/IML functions, the PLAN procedure in SAS/STAT software enables you to enumerate all combinations of elements, or to use random combinations in designing an experiment.
Furthermore, the SAS DATA step has multiple functions for working with combinations. The ALLCOMB function and several similar functions enable you to generate all combinations of elements that are contained in a DATA step array. The RANCOMB subroutine enables you to randomly permute elements in an array.
In summary, SAS software provides a "combination" of choices for choosing k items from a set of N possibilities.

16 Comments
It might be wise to go wild with RANCOMB! I believe ALLCOMB is spitting out the schedule in minimum change order, always with 2 toppings each lunch-time the same as the day before, so little variety of the salads on a day-to-day basis.
Perhaps there is a simple way of reordering the rows of the matrix that ALLCOMB outputs to maximize change?
That's right. Not much variety day-to-day, but the whole range of variety over 10 days. For more day-to-day variety, randomly permute the 10 rows that you get from ALLCOMB.
Thanks for this important post. This solved half of my problem. I am doing partial correlation of approx 40 variables taking two at a time and controlling for rest i.e.
Proc Corr data=test;
var Var1 Var2;
partial Var3 ....to ... Var40;
but I have to repeat it for all the combination that we can get using the method you have shown here i.e. N=40, k=2. The total combinations turns up to be a lot. Now I am wondering is there a short way of doing it i.e. with a macro do loop etc?
Thanks in advance
An interesting problem. Post it to the SAS Support Community for Statistical Procedures. In your post, include how many observations you have, since that will make a difference as to whether to use a macro, a BY statement, or some other approach.
I'm very curious how i can use this in a choice-based conjoint design study.
I have 6 attributes each with different levels.
This is the code that I use to get all the levels mixed and to get a good design.
Where and which code do I need to change the order of the 6 attributes of the design per choice set?
%mktruns (3**3 4**3)
%mktex (3**3 4**3, n=48, seed=17)
%mktlab (data=design, int=f1-f3)
%choiceff (data=final, model=class(x1-x6), nsets=16, flags=f1-f3, beta=1 0 0 0 0 0 3 2 1 3 2 1 -3 -2 -1)
proc print; id set; by set; run;
I don't fully understand your question and I don't see how the market macros match what you are say you are doing. If you are asking about listing attributes in varying orders when you administer the questionnaire, you can use %MktBIBD. Probably you should post this question to the SAS Support Community for Statistical Procedures, since it is fundamentally a question about experimental design.
Pingback: Lexicographic combinations in SAS - The DO Loop
Pingback: The best articles of 2013: Twelve posts from The DO Loop that merit a second look - The DO Loop
Is there a way to generate these combinations without using SAS/IML? My company just discontinued IML and now my code (as is) is no longer repeatable.
The second-to-last paragraph contains links to DATA step functions. You can also see the article "Lexicographic combinations."
Hello, Rick:
Could you advise what happen if I have multiple rows for Items, and would like to have all different combinations for each row of the item? FInally, I would like to append all rows, how can I do so? Thank you for any advice.
proc iml;
N=5;
k=3;
idx = allcomb(N, k);
Items = {"Broccoli" "Carrots" "Cucumbers" "Peppers" "Tomatoes",
"Chicken" "Beef" "Pork" "Duck" "Lamb",
"Water" "Apple Juice" "Wheat Grass" "Orange Juice" "Soda"};
C1=Items[1,];
C2=Items[2,];
S1 = C1[,idx];
S1 = shape(S1,0,k);
S2 = C2[,idx];
S2 = shape(S2,0,k);
S3 = C3[,idx];
S3 = shape(S3,0,k);
D=S1//S2//S3;
print Items C1 C2 C3 S1 S2 S3 D;
quit;
Your code looks fine, except you forgot to define
C3=Items[3,];
I hope that answers your question, but if not please post your question at the SAS/IML Support Community. The Community has many experts and is better suited for posting code and attachments.
Hi
is it possible to use values from a matrix:
i.e. asking to generate the combination of values from a particular matrix,
instead of defining the items as follows:
Items = {"Broccoli" "Carrots" "Cucumbers" "Peppers" "Tomatoes",
"Chicken" "Beef" "Pork" "Duck" "Lamb",
"Water" "Apple Juice" "Wheat Grass" "Orange Juice" "Soda"};
???
Thanks,
K
The ALLCOMB function always generates an integer matrix that you can use as indices to another matrix. The RANCOMB function can generate random combinations of a vector, as shown in the doc.
I don't know how to interpret "combinations from a matrix." Perhaps you are asking about the ExpandGrid function. You might want to ask your question on the SAS Support Communities and include the output that you want to see.
Hi Rick,
suppose my Items are made of 2 Broccolis and 3 Carrots, for a total of 5 items.
Is it possible to create a list with repeating items without writing them manually?
Thanks.
If I understand the question, you have two sets, one with N1 items and the other with N2 items. You are trying to
find the unique enumerations of three items where i items (0<=i<=N1) are from the first set and j items (0<=j<=N2) are from the second set. So you want to find integer points (i,j) that satisfy the constraints
i+j = 3
0 <= i <= N1
0 <= j <= N1
You can solve this as a feasibility problem or by enumerating all (i,j) pairs where 0 <= i <= N1 and 0 <= j <= N1, and then searching the space for solutions where i+j=3.