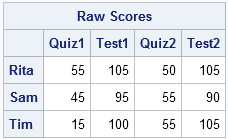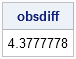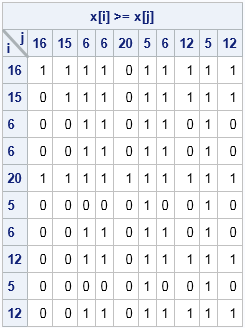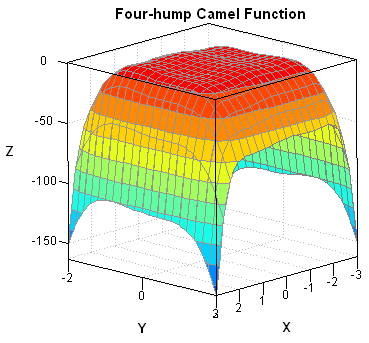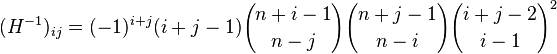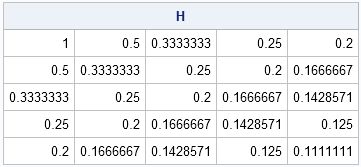
Last week I received a message from SAS Technical Support saying that a customer's IML program was running slowly. Could I look at it to see whether it could be improved? What I discovered is a good reminder about the importance of vectorizing user-defined modules. The program in this blog
Like most programming languages, the SAS/IML language has many functions. However, the SAS/IML language also has quite a few operators. Operators can act on a matrix or on rows or columns of a matrix. They are less intuitive, but can be quite powerful because they enable you perform computations without
My colleagues at the SAS & R blog recently posted an example of how to program a permutation test in SAS and R. Their SAS implementation used Base SAS and was "relatively cumbersome" (their words) when compared with the R code. In today's post I implement the permutation test in
My previous blog post describes how to implement Conway's Game of Life by using the dynamically linked graphics in SAS/IML Studio. But the Game of Life is not the only kind of cellular automata. This article describes a system of cellular automata that is known as Wolfram's Rule 30. In
A SAS customer showed me a SAS/IML program that he had obtained from a book. The program was taking a long time to run on his data, which was somewhat large. He was wondering if I could identify any inefficiencies in the program. The first thing I did was to
Nonlinear optimization routines enable you to find the values of variables that optimize an objective function of those variables. When you use a numerical optimization routine, you need to provide an initial guess, often called a "starting point" for the algorithm. Optimization routines iteratively improve the initial guess in an
Bootstrap methods and permutation tests are popular and powerful nonparametric methods for testing hypotheses and approximating the sampling distribution of a statistic. I have described a SAS/IML implementation of a bootstrap permutation test for matched pairs of data (an alternative to a matched-pair t test) in my paper "Modern Data
Just one last short article about properties of the Hilbert matrix. I've already blogged about how to construct a Hilbert matrix in the SAS/IML language and how to compute a formula for the determinant. One reason that the Hilbert matrix is a famous (some would say infamous!) example in numerical
The Hilbert matrix is the most famous ill-conditioned matrix in numerical linear algebra. It is often used in matrix computations to illustrate problems that arise when you compute with ill-conditioned matrices. The Hilbert matrix is symmetric and positive definite, properties that are often associated with "nice" and "tame" matrices. The
Vector languages such as SAS/IML, MATLAB, and R are powerful because they enable you to use high-level matrix operations (matrix multiplication, dot products, etc) rather than loops that perform scalar operations. In general, vectorized programs are more efficient (and therefore run faster) than programs that contain loops. For an example
