In a previous blog, I showed how to use SAS/IML subscript reduction operators to compute the location of the maximum values for each row of a matrix. The subscript reduction operators are useful for computing simple statistics for each row (or column) of a numerical matrix. If x is a
Tag: Efficiency
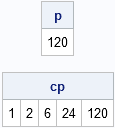
The birthday matching problem is a classic problem in probability theory. The part of it that people tend to remember is that in a room of 23 people, there is greater than 50% chance that two people in the room share a birthday. But the birthday matching problem is also
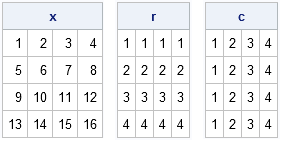
Sometimes in matrix computations you need to obtain the values of certain submatrices such as the diagonal elements or the super- or subdiagonal elements. About a year ago, I showed one way to do that: convert subscripts to indices and vice-versa. However, a tip from @RLangTip on Twitter got me
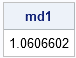
I recently blogged about Mahalanobis distance and what it means geometrically. I also previously showed how Mahalanobis distance can be used to compute outliers in multivariate data. But how do you compute Mahalanobis distance in SAS? Computing Mahalanobis distance with built-in SAS procedures and functions There are several ways to
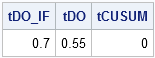
Way back when I learned to program, I remember a computer instructor explaining that an IF-THEN statement can be a relatively slow operation. He said "If a multiplication takes one unit of time, an IF statement requires about 70 units." I don't know where his numbers came from, or even
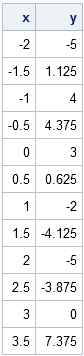
Polynomials are used often in data analysis. Low-order polynomials are used in regression to model the relationship between variables. Polynomials are used in numerical analysis for numerical integration and Taylor series approximations. It is therefore important to be able to evaluate polynomials in an efficient manner. My favorite evaluation technique
NOTE: SAS stopped shipping the SAS/IML Studio interface in 2018. It is no longer supported, so this article is no longer relevant. When I write SAS/IML programs, I usually do my development in the SAS/IML Studio environment. Why? There are many reasons, but the one that I will discuss today
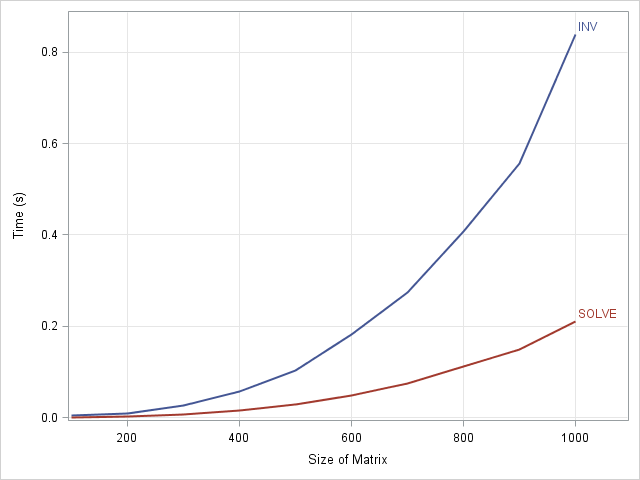
I've previously described ways to solve systems of linear equations, A*b = c. While discussing the relative merits of the solving a system for a particular right hand side versus solving for the inverse matrix, I made the assertion that it is faster to solve a particular system than it

This article describes the SAS/IML CHOOSE function: how it works, how it doesn't work, and how to use it to make your SAS/IML programs more compact. In particular, the CHOOSE function has a potential "gotcha!" that you need to understand if you want your program to perform as expected. What
The SAS/IML language provides two functions for solving a nonsingular nxn linear system A*x = c: The INV function numerically computes the inverse matrix, A-1. You can use this to solve for x: Ainv = inv(A); x = Ainv*c;. The SOLVE function numerically computes the particular solution, x, for a
