Rick Wicklin, PhD, is a distinguished researcher in computational statistics at SAS and is a principal developer of SAS/IML software. His areas of expertise include computational statistics, simulation, statistical graphics, and modern methods in statistical data analysis. Rick is author of the books Statistical Programming with SAS/IML Software and Simulating Data with SAS.
Occasionally a SAS statistical programmer will ask me, "How can I construct a large correlation matrix?" Often they are simulating data with SAS or developing a matrix algorithm that involves a correlation matrix. Typically they want a correlation matrix that is too large to input by hand, such as a
Dear Rick, I have a data set with 1,001 numerical variables. One variable is the response, the others are explanatory variable. How can I read the 1,000 explanatory variables into an IML matrix without typing every name? That's a good question. You need to be able to perform two sub-tasks:
Last week I discussed ordinary least squares (OLS) regression models and showed how to illustrate the assumptions about the conditional distribution of the response variable. For a single continuous explanatory variable, the illustration is a scatter plot with a regression line and several normal probability distributions along the line. The
I've previously written about how to generate a sequence of evenly spaced points in an interval. Evenly spaced data is useful for scoring a regression model on an interval. In the previous articles the endpoints of the interval were hard-coded. However, it is common to want to evaluate a function
A friend who teaches courses about statistical regression asked me how to create a graph in SAS that illustrates an important concept: the conditional distribution of the response variable. The basic idea is to draw a scatter plot with a regression line, then overlay several probability distributions along the line,
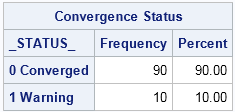
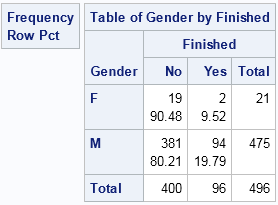
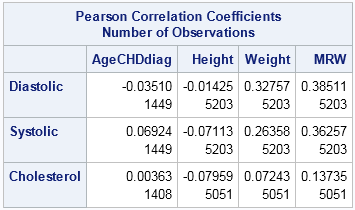
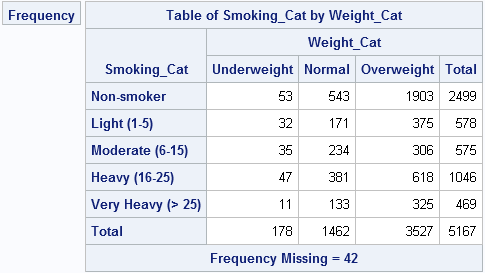
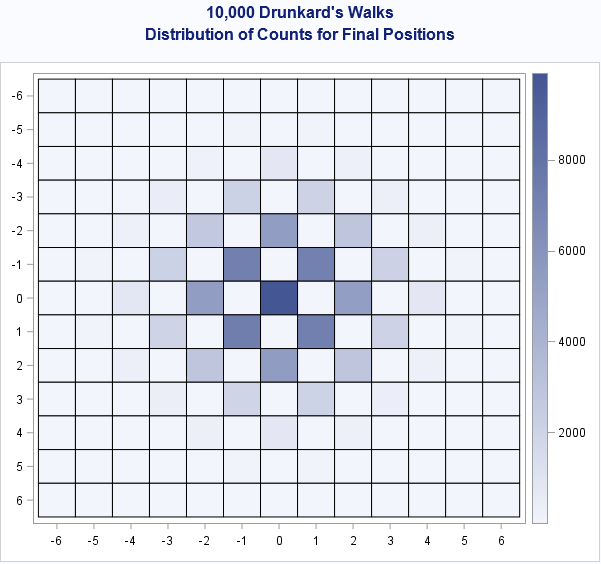
Statistical programmers often have to use the results from one SAS procedure as the input to another SAS procedure. Because ODS enables you to you to create a SAS data set from any ODS table or graph, it is easy to obtain a data set that contains the value of
In my previous blog post, I showed how you can use SAS to program a "weaving" algorithm that takes an image, cuts it into strips, and weaves the strips together to create mathematical art. I used matrices and heat maps for the computations and visualization. At the end of the
An artist friend of mine recently created a beautiful abstract image and described the process on her blog. She says that "after painting my initial square, I cut it into strips and split them down the middle, then wove them together.... I had no idea when I started piecing these
The title of this blog post might seem strange, but I occasionally need to compute the number of digits in a number, usually because I am trying to stuff an integer value into a string. Each time, I have to derive the formula from scratch, so I am writing this
Ugh! Your favorite regression procedure just printed a warning to the SAS log. Something is wrong, and your attempt to fit a model to the data has not succeeded. A typical message is "WARNING: The validity of the model fit is questionable," perhaps followed by some additional diagnostic messages about
