A previous article shows how to implement recursive formulas in SAS. The article points out that you can often avoid recursion by using an iterative algorithm, which is more efficient. An example is the Fibonacci sequence, which is usually defined recursively as
     F(n) = F(n-1) + F(n-2) for n > 2,
where the base cases are defined as F(1)=1 and F(2)=1. However, the sequence can be computed directly (and more efficiently) by storing the first two values in an array and then using an iterative loop to define subsequent values.

While showing how to emulate recursion in the SAS IML language, I wrote, "a straightforward recursive formula recomputes the same quantity many times.... You can make the computation much more efficient if you store these values after they are computed and look them up as needed." This becomes important if each function performs a long and complex computation. A fundamental principle of efficient programming is to not repeat long computations. If you compute some quantity that you will need again, you should store it and retrieve it when needed.

This article shows how you can use a global variable to cache values of the Fibonacci sequence. When you make a function call, the function first looks to see if the resulting value is stored from a previous computation. If so, it uses them. If not, it computes the value and stores it.

Cache values of the Fibonacci sequence

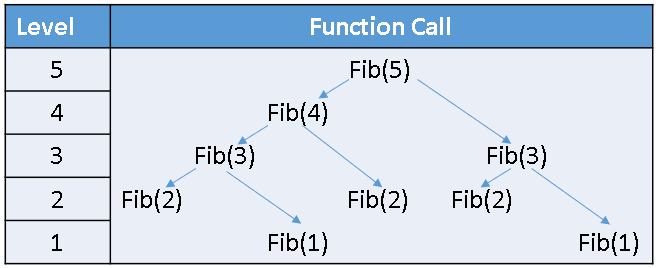
The SAS IML language does not support recursive function calls. However, a previous article shows how to use the SAS macro language to emulate recursion by generating SAS IML functions that have different names, F1, F2, F3, .... The "higher-level" functions (for example, F5) calls lower-level functions (for example, F4 and F3), which in turn call even lower lower-level functions, as shown in the diagram to the right.

The recursive definition is inefficient because it results in many function calls. For example, to compute the 15th term of the Fibonacci sequence requires 3,177 function calls! For the Fibonacci sequence, each function call performs only one addition, so the computation is seemingly fast. But for computations that are more time consuming, it makes sense to store and retrieve the low-level values so they can be reused. In the SAS DATA step or in the SAS IML language, you can use arrays to store previously computed values.

The following SAS macro modifies the macro in the previous article by adding a GLOBAL statement to each function. All functions (except the base cases) use the same global vector. When the i_th function is called, it checks whether the i_th element of the vector is nonmissing. If so, it returns the value. Otherwise, it computes the value and stores it. To use the function, you must call the macro and specify the maximum number of terms in the Fibonacci sequence. The macro generates the functions and allocates the global vector. You can then call the functions to generate the Fibonacci sequence. The following program generates 20 terms by defining 20 IML functions. The higher-level functions call the lower-level functions.

/* Define functions that emulate recursion.
   Use a global variable to cache values of the Fibonacci 
   sequence that have been previously computed.
*/
%macro DefineFibFuncsEfficient(n);
   /* define the base cases, F1 and F2 */
   start F1(d=0);  
      return 1;
   finish;
   start F2(d=0);
      return 1;
   finish;
   /* define the recursive functions: F_i calls F_{i-1} and F_{i-2} */
%do i = 3 %to &n;
   start F&i.(d=0) global(g_FibSeq);
      /* if global vector doesn't has the value, compute it and store it */
      if g_FibSeq[&i]=. then 
         g_FibSeq[&i] = F%eval(&i-1)() + F%eval(&i-2)();
      return( g_FibSeq[&i] );
   finish;
%end;
   g_FibSeq = j(1,&n,.);  /* create the global vector */
   g_FibSeq[1:2] = 1;     /* initial base cases */
%mend;
 
proc iml;
%DefineFibFuncsEfficient(20);    /* define the functions up to F20 */
Fib20 = F20();                   /* compute 20th term, which computes all earlier terms */
FibSeq = g_FibSeq;               /* get sequence from global vector */
labls = 'F1':'F20';
print FibSeq[c=labls];

The computation is still inefficient and requires many function calls, but at least it doesn't recompute the same values over and over again!

This example shows how to improve the efficiency a recursive formula. I would never use this code to generate the Fibonacci sequence, but I did use similar code to generate the PDF of a discrete probability distribution that was defined recursively. Before caching the values, the distribution computation was very slow, and I could only compute five recursive levels. After caching the values, I was able to easily compute 20 or even 50 levels of recursion.

Summary

I am not a fan of using recursion, but sometimes it is convenient. This article emphasizes that a recursive formula can be computed more efficiently if you store each intermediate computation and reuse it for subsequent function calls. I illustrate the idea by emulating recursion in the SAS IML language and using a GLOBAL variable to cache the results of each step of a recursive computation.

This trick works only if the functions return the same value every time they are called. Some recursive algorithms take input arguments that change at each step (for example, Merge Sort or Quick Sort). For those algorithms, you cannot cache previous values.