There are two programming tools that I rarely use: the SAS macro language and recursion. The SAS macro language is a tool that enables you to generate SAS statements. I rarely use the SAS macro language because the SAS IML language supports all the functionality required to write complex programs, including user-defined functions. Also, I rarely use recursion. There are two reasons. First, although recursion is supported for user-defined functions in PROC FCMP, which can be called from the DATA step, the SAS IML language does not support recursion. Second (and more importantly, many recursive algorithm can be implemented by using iteration, which tends to be faster and require less memory.

However, recently I saw a recursive formula for a discrete probability distribution. Because I was interested in the distribution, I had to ponder how to implement the recursive formula in the SAS IML language. I settled on using the SAS macro language, which enables me to generate the definition of many SAS IML functions, which I could then call to compute the distribution.

I'll save a discussion of the probability distribution for another day. In this article, I will demonstrate how you can use SAS macro to emulate a recursive formula in the SAS IML language. This is NOT an efficient way to solve the problem, but it is an interesting application of the macro language that is worth sharing.

The Fibonacci recursion formula

A famous recursion formula is the definition of the Fibonacci sequence. (The factorial function is another famous example.) The nth term of the Fibonacci sequence is defined in terms of the two previous terms. If F(n) is the function that gives the nth term, then
     F(n) = F(n-1) + F(n-2) for n > 2,
where the base cases are defined as F(1)=1 and F(2)=1. By using this formula, you can determine that the first few terms of the Fibonacci sequence are 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

Although the definition uses recursion, there are many efficient ways to generate the sequence without using recursion. I have previously written about five ways to handle recurrence relations in SAS, and not one requires writing a recursive function. But, for the sake of the discussion, let's see how to implement a recursive formula in Base SAS. You can use the FCMP procedure to implement a user-defined function that is recursive. It is less efficient than the methods I discuss in the previous article, but here is the recursive formula implemented by using the DATA step:

/* PROC FCMP supports recursion */
proc fcmp outlib=work.funcs.math;
   function Fib(n);
      if n = 1 then return(1);
      else if n = 2 then return(1);
      else return(Fib(n-1) + Fib(n-2));  /* recursion */
   endsub;
run;
 
options cmplib=work.funcs;
data FibonacciSequence;
   do n = 1 to 10;
      Fib = Fib(n);
      output;
   end;
run;
 
proc print data=FibonacciSequence noobs;
run;

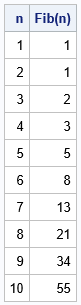
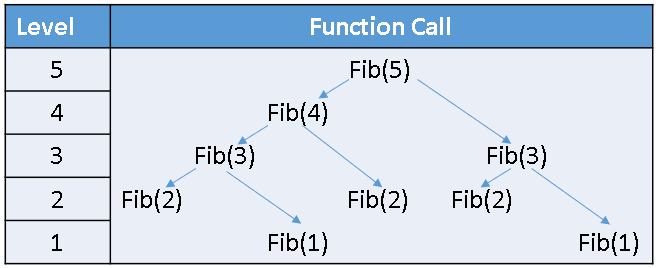
The answers are as we expect, but this implementation is not efficient? Why? Well, for one reason, the program continuously re-computes quantities that it has previously computed. A fundamental principle of efficient programming is to compute something once and remember it if you need that quantity again. Let's examine what the recursive function call does when you call Fib(5):

• There is 1 call to Fib(5), which calls Fib(4) and Fib(3).
• The call to Fib(4), makes calls to Fib(3) and Fib(2). Thus, in all, there are two calls to Fib(3).
• The two calls to Fib(3) each make a call to Fib(2) and a call to Fib(1). Thus, in all, there are 3 calls to Fib(2) and 2 calls to Fib(1).
• The calls to Fib(2) and Fib(1) each return a value.

Thus, calling Fibonacci(5) results in many function calls, as shown in the following schematic diagram. A straightforward recursive formula recomputes the same quantity many times, whereas an iterative implementation of the Fibonacci sequence saves the intermediate results and looks them up as needed.

Recursive functions in SAS IML

The SAS IML language does not support recursive calls. However, you can emulate recursion by defining a sequence of functions that have DIFFERENT NAMES, such as F1, F2, F3, and so forth. The F1 and F2 functions can return 1 (the base case), whereas the F3 function can return the sum of the results from calling F1 and F2. You can continue this process as shown in the following program. Notice that I use a dummy variable with a default value so that each function can be called without specifying any arguments.

/* Many sources use a recursive definition for the Fibonacci sequence:
   F(i) returns the i_th Fibonacci number, 
   F(i} = F(i-1) + F(i-2) for i > 2, and F(1)=F(2)=1.
 
   We can't use use recursion in IML, but you can emulate it.
   Move the argument to the subscript and define 
   F_i() = F_{i-1}() + F_{i-2}() for i > 2.
*/
proc iml;
/* define the base cases */
start F1(d=0);
   return 1;
finish;
start F2(d=0);
   return 1;
finish;
/* define the cases that use previous values in the sequence */
start F3(d=0);
   return F2() + F1();
finish;
start F4(d=0);
   return F3() + F2();
finish;
start F5(d=0);
   return F4() + F3();
finish;
start F6(d=0);
   return F5() + F4();
finish;
 
R = F1() ||  F2() ||  F3() ||  F4() ||  F5() ||  F6();
labls = 'F1':'F6';
print R[c=labls];

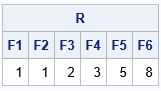
Generating IML code by using SAS macro

I got tired and bored after defining the 6th function. Notice that all the functions F3 through Fn follow the same template. That makes them ideal candidates to be generated automatically. In SAS, there are two ways to write a program that generates SAS statements:

• SAS macro language: Use the macro language when all program statements are known before you need to run the program. That is the case here. We know exactly what each function looks like, we just need help writing many functions.
• CALL EXECUTE: Use CALL EXECUTE when you don't know some of the program statements until run time. That is, you need run-time data or the value of certain variables in order to write the program.

It isn't hard to use the SAS macro language to generate a lot of function definitions that all follow the same template. The following macro generates the code for the F1 and F2 functions, then uses a %DO macro loop to generate higher-order function definitions. The %EVAL macro generates the numbers &i-1 and &i-2 for each value of i in the macro %DO loop, as follows:

/* Use a dummy variable b/c IML doesn't allow functions 
   that have zero arguments */
%macro DefineFibFuncs(n);
   start F1(d=0);  
      return 1;
   finish;
   start F2(d=0);
      return 1;
   finish;
%do i = 3 %to &n;
   start F&i.(d=0);
      return( F%eval(&i-1)() + F%eval(&i-2)() );
   finish;
%end;
%mend;
 
proc iml;
%DefineFibFuncs(10); /* define functions F1, F2, ..., F10 */
/* what is the 10th Fibonacci number? Call F10, which calls F9 and F8, which call other functions */
Fib10 = F10();       
print Fib10;

Notice that, as written, the F10 function is very slow. A call to the F10 function ends up calling and re-computing the values for F8, F7, ..., F3 many times. You can make the computation much more efficient if you store these values after they are computed and look them up as needed.

Summary

The SAS IML language does not support recursive function calls. In general, recursion can be slow and inefficient. However, I recently encountered a situation in which it was expedient to use recursion, so I used the SAS macro language to write a series of IML functions that emulate recursion. To illustrate the process, I used the familiar example of the Fibonacci sequence. I've previously shown how to compute the Fibonacci sequence without using recursion. In this article, I demonstrate recursion in the DATA step, and I show how to use the SAS macro language to emulate recursion in SAS IML programs. The resulting program is not very efficient. It could be improved by computing each function once, storing the result, and then reusing the result upon subsequent function calls. I will demonstrate that technique in a subsequent article.