Rockin' around the Christmas tree,
Have a happy holiday
     – Brenda Lee

An internet search for "How many lights do I need for my Christmas tree," returns many opinions. A popular answer is that you need "one strand of lights for each foot of your tree." Another common answer is "100 mini lights per vertical foot." However, strands vary in length. Furthermore, these easy-to-remember rules consider only the height of the tree. They ignore a fundamental fact of Christmas tree geometry: The tree is approximately a cone. If the base of the tree has a wide radius, you will need more lights than if the base of the tree has a small radius. Thus, when calculating the length of a string of lights for a Christmas tree, you should account for the shape of the tree, which includes both the height and the radius of the lowest branches. (Technically, the full tree height doesn't matter, only the height from the lowest branches to the top.)

I recently saw a post on social media that used math to compute the length of a helical string of lights wrapped on a perfectly conical Christmas tree that has height H and radius of the base R. Again, H measures only the "green" part of the tree, from the bottom of the first set of branches to the top of the tree. The formula is given in the next section. It is very complicated.

I think there is a better mathematical model that is simpler and for which the length of the lights is easier to compute. I call it the n-rings model. For the n-rings model, you first wrap the lights around the lowest set of branches. This makes a horizontal ring around the tree. You then pass the string up to the next set of branches and wrap the lights horizontally around the tree on that set of branches. You continue this process a total of n times until you wrap the lights around the last set of branches near the top of the tree. The length of the string of lights needed for this process is simple to evaluate by using a handheld calculator (or the calculator app on your phone).

You can use any units in these formulas. This article uses "feet" because that is the US measurement used for Christmas tree heights and for strings of lights.

The helical model of stringing lights

The helical model for stringing lights looks like the images below. In these images, a string of lights wraps around a perfectly conical tree with base radius R and branch-height H. The branch-height measures the height from the lowest branch to the top of the tree. It excludes the trunk and tree stand. In the images, n=10, R=2, and H=5.

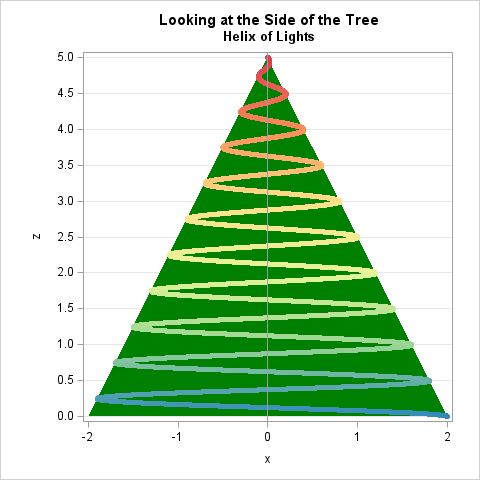
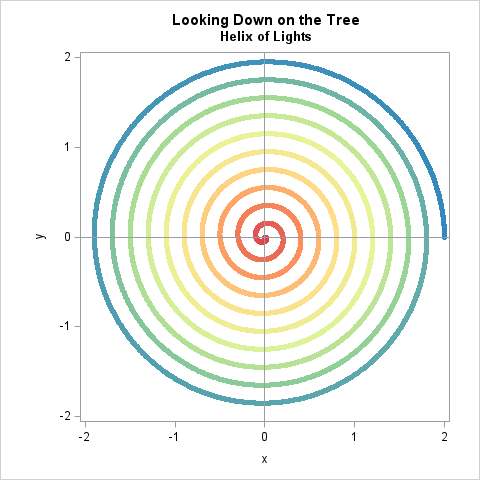
The string of light progresses up the tree at a constant rate. The lights wrap around the tree a total of n times. In the images, n=10. For any value of n, the social media post claims that the formula for the length of the lights is given by the following complicated expression:
$L_\mbox{Helix} = \frac{H}{2} \sqrt{1+R^2(1+(2\pi n)^2)} + \frac{H(1+R^2)}{4\pi n R} \sinh^{-1} \left(\frac{2\pi n R}{\sqrt{1+R^2}}\right)$

Yuck! Not only is this formula complicated, but it involves the function "$\sinh^{-1}$," which is called the "inverse hyperbolic sine" function. Some simple calculators do not even contain a key for this function, although most scientific calculators can compute this function by combining a "2nd" or "inverse" key with the "sinh" key. If your calculator doesn't support this function, you can use the identity $\sinh^{-1}(x) = \log\left(x + \sqrt{x^2 + 1}\right)$. No matter how you express it, the formula is complicated to use. The formula can be derived by parameterizing the helix and applying the arclength formula from multivariable calculus.

In this article, I use the second formula. In the images, the length of the helical string of lights wrapped n=10 times is 63.33 feet.

The n-rings model of stringing lights

The helical model is not always an accurate model of how people string lights on their tree. I use the n-rings approach, perhaps because I have an artificial tree for which the branches are more or less aligned in rows. My tree has a total of 12 rings of branches that are about 6 inches apart, so it is natural to wrap each set of branches with lights. The n-rings model for stringing lights looks like the images below, which again use R=2 and H=5.

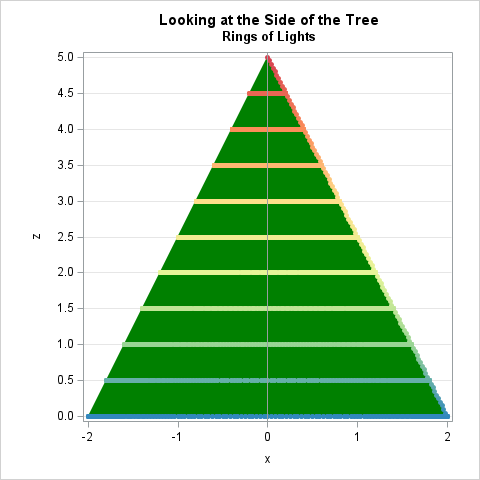
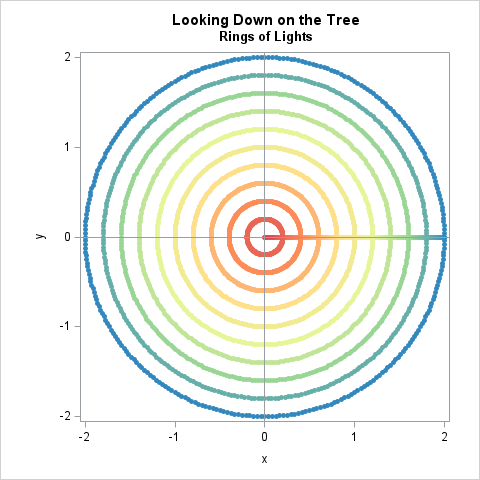
In the images, n=10 because there are 10 horizontal rings of lights. Each ring is connected by a slanted vertical segment that connects each horizontal ring to the next one above it. (I put the vertical segment of light on the back of the tree.) For any value of n, the formula for the length of the lights is given by the following simple expression:
$L_\mbox{Rings} = \sqrt{R^2 + H^2} + (n+1) \pi R$

Ah! This formula is much simpler! In the images, the length of the string of lights in the n-rings model is 74.50 feet when n=10. Notice that this length is longer than the length for the helical model. This is always the case. Therefore, you can always use the simpler n-rings formula if you are trying to estimate how many boxes of lights you'll need for a conical tree of a given height and base radius. For the math nerds, the formula is derived in the Appendix.

A SAS program to compute the length of Christmas tree lights

You can write a program to compute length of lights for the two models. I think that placing lights about 6 inches (0.5 feet) apart looks nice, so for a tree that has height H, I suggest winding the lights around the tree n = ceil(2*H) times. (Math comment: The formulas don't care whether n is an integer. They still make sense if you want to wrap the lights 10.5 times!)

/* SAS DATA step to compute the length of strings of lights for two 
   strategies for winding them onto a conical Christmas tree: 
   helical model and the n-rings model */
data LengthOfLights;
keep H R n L_Helix L_Rings;
label H = "Height of Branches (ft)"
      R = "Radius of Lower Branches (ft)"
      n = "Number of Rings"
      L_Helix = "Length of Helical Model"
      L_Rings = "Length of Rings Model";
format L_Rings 6.1 L_Helix 6.1;
input H R;
 
pi = constant('pi');
n = 2*H;           /* wind the lights twice per vertical foot */
s2 = R**2 + H**2;
s = sqrt(s2);      /* vertical (slant) length of tree (Pythagorean Theorem) */
 
/* 1. formula for arc length of helix */
w = 2*pi*n;
v = R * w;
L_Helix = 0.5*sqrt(s2 + v**2) + (s2/(2*v)) * arsinh(v/s);
 
/* 2. formula for rings with a vertical connection */
sum_Rings = (n+1)*pi*R;
L_Rings = s + sum_Rings; 
datalines;
3.5 1.5
4   1.5
4.5 1.5
5   2
5.5 2
5.5 2.5
6   2.5
6   3
;
 
proc print noobs data=LengthOfLights label; 
run;

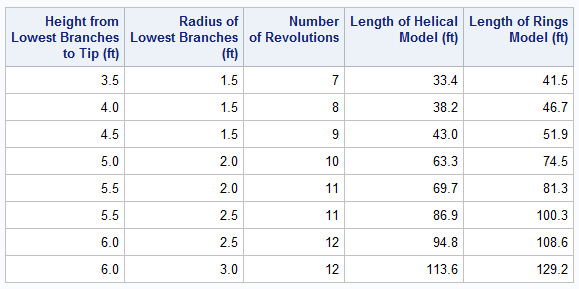
For the record, my family's (artificial) tree has H=5 feet and R=2 feet. The table says that the n-Rings method with n=10 requires 74.5 feet of lights. Accordingly, I use 8 boxes of 10-foot strings, which gives me 80 feet of lights. Because this is more length than I need for 10 rings, I let the lights undulate up and down as I wind them.

If you already have boxes of lights at home, you can invert the n-rings formula to solve for n. This tells you how many rings you can form if you have a string of length L. The inverse formula is
$n = (L - s)/(\pi R) - 1, \,\mbox{where}\, s = \sqrt{R^2 + H^2}$
For example, I have L=80 feet of lights, so for R=2 and H=5 I could wrap the tree 10.88 times by using equidistant rings.

Summary

This article considers the question, "How many lights do I need to wrap around my Christmas tree." Common online answers use only the height of the tree, not the radius of the base.

A better answer uses the base radius. One online formula is for a mathematical model in which the light strings are wrapped in a helix. The helical formula is very complicated, and for some trees, a helical winding might not be practical.

This article presents a simple mathematical model, which is the n-rings model. This model is appropriate for artificial trees or a natural tree for which the branches look like stack of horizontal disks. You can wrap the lights around the lowest branches, transition to the next level, wrap the lights around the branches at that level, and continue until you reach the top of the tree. For any conical-shaped tree, measure the following:

• R: The radius of the lowest branches (from the trunk to the outer branches)
• H: The vertical distance up the trunk from the lowest branch to the top of the tree.

Appendix: Derivation of the n-rings formula

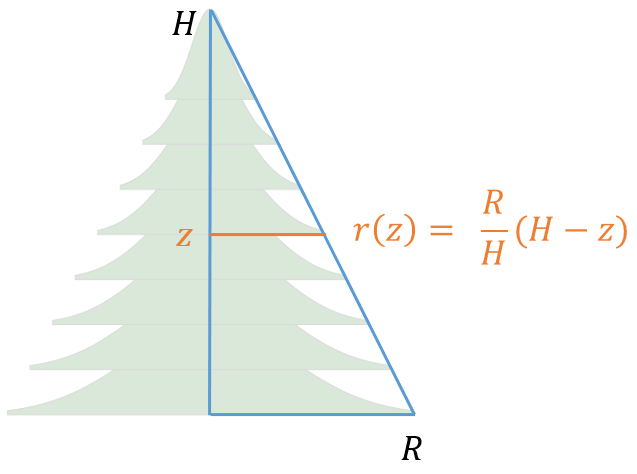
We want to find the total sum of circumferences for n circles that are equidistant on a right circular cone of height H and base radius R. The height between adjacent circles is dz = H/n. As shown in the image at the top of this article, if the first circle is at z=0, the radius of the i_th circle is
$r_i = \frac{R}{H}(H - z_i) \,\mbox{where}\, z_i = (i - 1)H/n$

Each circle has circumference $L_i = 2 \pi r_i$, so the total length of the circles is
$L = 2 \pi \frac{R}{n} \sum_{i=1}^n \left( n - i + 1 \right)$

There are some convenient formulas that simplify this formula:

• $\sum_{i=1}^n 1 = n$
• $\sum_{i=1}^n i = n (n+1)/2$
• $\sum_{i=1}^n n = n \sum_{i=1}^n 1 = n^2$

By applying these formulas, the summation signs vanish and we are left with the sum of the circumferences of the n circles:
$L = \pi R (n + 1)$

This is the length of the n equi-spaced circles. We can add in the sum of the lengths of the slanted segments that connect the circles. The union of those segments is the hypothesis of the right triangle, which, by the Pythagorean theorem, has the length $\sqrt{R^2 + H^2}$. Consequently, the total length of lights that are wrapped n times arounds a right circular cone of height H and radius R is
$L_{\mbox{Rings}} = \sqrt{R^2 + H^2} + (n + 1) \pi R$