In a previous post, I described ways to create SAS/IML vectors that contain uniformly spaced values. The methods did not involve writing any loops.

This post describes how to perform a similar operation: creating evenly spaced values on a two-dimensional grid. The DATA step solution is simple, but an efficient SAS/IML solution requires thinking about the problem in terms of vectors and matrices.

The DATA Step Solution

A grid of values is useful in many contexts, such as scoring and visualizing a statistical model. In the DATA step, you can use loops to create a grid of values. For example, to generate a 3 x 2 grid of values on the rectangle [0,2] x [0,1] you can use the following program:

data grid;
keep x y;
/** set parameters for the general problem **/
XMin = 0; XMax = 2; Nx = 3;
YMin = 0; YMax = 1; Ny = 2;
 
dx = (XMax-XMin)/(Nx-1);
dy = (YMax-YMin)/(Ny-1);
do y = YMin to YMax by dy;
   do x = XMin to XMax by dx;
      output;
   end;
end;
run;
 
proc print; var x y; run;

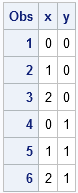
This solution uses a double loop to compute the values on a uniform grid. There are Nx points in the X direction, evenly spaced on the interval [XMin, XMax], and Ny points in the Y direction, evenly spaced on the interval [YMin, YMax].

As I've written before, the SAS/IML language is a vector-matrix language, and an efficient SAS/IML program is one that avoids writing unnecessary loops. How can you write a similar program in PROC IML that avoids one or both loops?

A SAS/IML Language Solution

UPDATE 2014: In SAS/IML 12.3 (released with SAS 9.4), you can use the EXPANDGRID function to generate a grid in multiple dimensions! The following program is not needed if you have a recent version of SAS.

There are three simple SAS/IML functions that you can use to create a module that computes a grid of evenly spaced values:

• The DO function for generating sequential values, which is described in a previous post.
• The REPEAT function, which repeats a pattern a specified number of times.
• The SHAPE function, which reshapes a vector into a matrix. I also wrote a previous post on reshaping matrices.

The first step is to use the parameters in the problem to determine the points in the X and Y directions that will form the grid:

proc iml;
XMin = 0; XMax = 2; Nx = 3;
YMin = 0; YMax = 1; Ny = 2;
XDiv = do(XMin, XMax, (XMax-XMin)/(Nx-1));
YDiv = do(YMin, YMax, (YMax-YMin)/(Ny-1));
print XDiv, YDiv;

These are the coordinates of the grid points, but you need to arrange them into a matrix of ordered pairs that contains Nx * Ny rows and 2 columns.

The X coordinates are easy to construct. To form the X coordinates you can repeat the XDiv vector Ny times, and then reshape those values into a column vector:

X = repeat(XDiv, Ny);
X = shape(X, Nx*Ny);  /** or use COLVEC module in IMLMLIB **/
print X;

The Y coordinates are a little more difficult to construct. Recall that SAS/IML matrices are stored row-wise. This means that if you use the REPEAT function to form a set of points from the YDiv vector, the points will be in the wrong order:

Y = repeat(YDiv, Nx);
print Y; /** wrong order: elements stored row-wise **/

What you really want is to traverse the Y matrix down the columns instead of across the rows. No problem! Use the T function to transpose the values, and then reshape those transposed values into a column:

Y = shape(T(Y), Nx*Ny);  /** or use COLVEC module in IMLMLIB **/

A SAS/IML Module That Defines Ordered Pairs on a Grid

You can put these statements into a module, which enables you to conveniently generate a grid of points:

/** Module to define ordered pairs in a uniform grid of points.
   Input: XMin = minimum value of the X coordinate of the grid
          XMax = maximum value of the X coordinate of the grid
          Nx = number of grid lines along the X coordinate
          YMin = minimum value of the Y coordinate of the grid
          YMax = maximum value of the Y coordinate of the grid
          Ny = number of grid lines along the Y coordinate
 
    Output: Ordered pairs are returned in a matrix with
         (Nx x Ny) rows and two columns.
**/
start Define2DGrid(XMin, XMax, Nx, YMin, YMax, Ny);
   XDiv = do(XMin, XMax, (XMax-XMin)/(Nx-1));
   YDiv = do(YMin, YMax, (YMax-YMin)/(Ny-1));
   X = repeat(XDiv, Ny);
   X = shape(X, Nx*Ny);
   Y = repeat(YDiv, Nx);
   Y = shape(T(Y), Nx*Ny);
   return ( X || Y );
finish;
 
/** Example: Use the module to define a grid of points and 
      then evaluate a function f(x,y) on the grid. **/
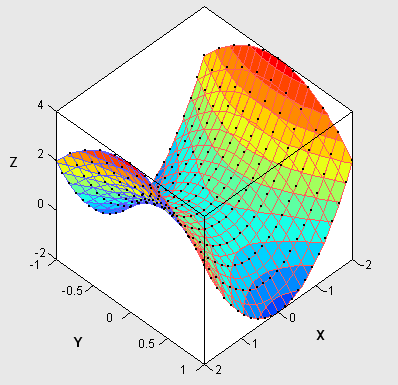
p = Define2DGrid(-2, 2, 23,  /** 23 points in [-2,2] **/
                 -1, 1, 11); /** 11 points in [-1,1] **/
x = p[,1];  y = p[,2];
z = x##2 - 2*y##2;  /** evaluate a function z = f(x,y) **/
 
/** the following SAS/IML Studio statement creates a rotating plot **/
RotatingPlot.Create("Quadratic Surface", x, y, z);