In many families, siblings draw names so that each family member and spouse gives and receives exactly one present. This year there was a little bit of controversy when a family member noticed that once again she was assigned to give presents to me. This post includes my response to her, followed by an analysis and a versatile program that fully automates the family gift exchange. I end with a challenge: can you create a gift exchange list that is better than mine?
Dear Pam,Thank you for the Christmas gifts. As usual, they were generous and superb.
During our recent family get-together, you commented that the Great Christmas Gift Exchange hasn't seemed very random to you. Specifically, you noted that my daughter (who pulls names out of a hat) has pulled my name to receive your gifts several times in recent years. You jokingly asked if we were involved in a conspiracy!
You then said something intriguing: "Perhaps we could automate the choice of names so that over a period of years each person in the family gives to everyone else and all combinations of giver-receiver occur."
Since I am a statistical programmer, I wrote a program to generate exactly what you asked for: all possible pairs of Givers and Receivers. However, this schedule requires 80 years to complete. So, I am instead including a simpler schedule in which each giver gives to a different person each year. (The letters represent the first initial of each person's name.) After eight years, we'll repeat. I think this captures the essence of your request.
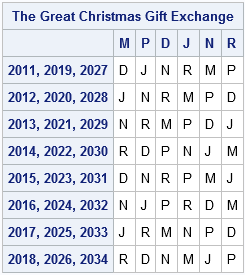
Thanks again for the wonderful gifts. I look forward to 2013 when your generosity flows my way once again.
Love,
RickP.S. Keep reading if you'd like to learn about the mathematics behind gift exchange lists!
A Gift-Exchange List is a Permutation
If you enumerate the family members in a standard order (say, oldest sibling to youngest, with each sibling followed by a spouse) and call that enumeration the Givers, then the Receivers are simply a permutation of the Givers. Thus, mathematically, the problem of creating a gift exchange is equivalent to generating permutations.
Although I eventually rejected the idea of sending Pam a comprehensive enumeration of all possible Giver-Receiver pairs, it is fun and instructive to see how to use the SAS/IML language to write a program that generates the complete list. The algorithm is straightforward:
- Generate all permutations of n elements, where n is the number of people involved in the gift exchange.
- For each permutation, determine if the permutation represents a valid exchange.
Feasible Permutations
Not every permutation is valid for a gift exchange. For example, no person should give to his spouse, nor to himself. The matrix of feasible Giver-Receiver pairs among n people can be represented by a matrix of zeros and ones in which Person i can give to Person j if and only if there is a one in the (i, j)th entry of the matrix.
My wife's family consists of three married siblings, so n=6 and each year I give to one of four people and receive from one of those same four. For this family, the feasible exchange matrix has a block structure that looks like this:
proc iml;
n = 6;
Valid = {0 0 1 1 1 1, /** Sibling 1 cannot give to self or spouse **/
0 0 1 1 1 1, /** Spouse 1 **/
1 1 0 0 1 1, /** Sibling 2 **/
1 1 0 0 1 1, /** Spouse 2 **/
1 1 1 1 0 0, /** Sibling 3 **/
1 1 1 1 0 0}; /** Spouse 3 **/ |
Permutation Matrices
You can represent each permutation by a permutation matrix which is a matrix of zeros and ones that maps the vector 1:n onto the permutation. For example, the permutation {3 4 5 6 1 2} represents the 2011 row in my letter to Pam. This permutation means that Person1 gives to Person3, Person2 gives to Person4, and so on. This permutation can be represented by the following permutation matrix:
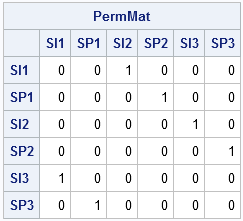
You can compute the permutation matrix by using the following SAS/IML statements:
/** create permutation matrix from permutation v **/
start GetPermutationMatrix(v);
n = ncol(v);
P = j(n, n, 0);
do i = 1 to n;
P[i, v[i]] = 1;
end;
return (P);
finish;
/** Sibling_1 ... Spouse_3 **/
names = {Si1 Sp1 Si2 Sp2 Si3 Sp3};
GiveTo = {3 4 5 6 1 2};
PermMat = GetPermutationMatrix(GiveTo);
print PermMat[r=names c=names]; |
Notice that this permutation is feasible because the locations of the ones in the permutation matrix correspond to ones in the Valid matrix. In contrast, the permutation {2 6 1 5 4 3} is not feasible for a gift exchange because the corresponding permutation matrix has a one in the (1, 2) position, which is not permitted by the Valid matrix.
Generating All Feasible Permutations
In a previous blog I showed how to generate a SAS data set that contains all permutations of n elements, so assume that Perm6 contains all possible permutations of 6 elements. You can iterate through the permutations and compare each permutation matrix with the Valid matrix in order to determine a complete set of permissible gift exchanges.
use perm6; read all var _NUM_ into X; close perm6;
v = j(1, n, .);
/** create data set to hold results **/
create matches from v;
do k = 1 to nrow(X);
v = X[k,]; /** get the kth permutation **/
P = GetPermutationMatrix( v );
s = sum(Valid#P); /** check whether permutation is valid **/
if s = n then /** if so, append to results **/
append from v;
end;
close matches; |
The matches data set contains the feasible permutations. For my wife's family, this consists of 80 rows, which means that it would require 80 Christmases to exhaust the list of all possible Giver-Receiver pairs.
No More Hats and Pieces of Paper
You can download the SAS program that generates the Gift-Exchange List. The program can also handle unusual circumstances such as the fact that Aunt Mildred refuses to give a gift to Joey because she has never forgiven him for crushing her prized begonias during the 1985 post-Christmas Family Football Game. You just need to add a zero to the Valid matrix in Aunt Mildred's row and Joey's column.
The list is in a systematic order, so randomize it before printing it out and distributing it to the relatives.
A Pretty Good Gift Exchange
Ultimately, I sent Pam a different schedule. Because the feasibility matrix in our family has a block structure, I can write down a small four-year schedule (2011–2014) in which each person gives to his or her four feasible receivers. But that the schedule is not diverse in the combinations of receivers. For example, my wife and I (the last two columns) give to the combination M+P and M+J during 2011–2014, but we don't give to the combination M+D. We also do not give to other combinations, such as P+J. In an attempt to address that issue, I created a second four-year schedule (2015–2018) and appended it to the first.
Is it perfect? No, but it's pretty good and it satisfies Pam's desire to not give to the same person two years in a row. In fact, the only repeats I see happen in 2019 (and every eight years after that) when D gives to N and R gives to P.
A Challenge
Can you create a better schedule than the one that I sent Pam? The ultimate eight-year schedule would be one in which no Giver-Receiver pair is the same as the immediately preceding year. Does such a schedule exist? If not, can you create an eight year schedule in which only a single Giver-Receiver pair is the same as the immediately preceding year?

12 Comments
Pingback: Simulating a Christmas Gift Exchange - The DO Loop
Pingback: Matrices and mattresses - The DO Loop
Here is a way to generate the 80 permutations using PROC CLP in SAS/OR:
proc clp out=out allsolns; var (X1-X6) = [1,6]; alldiff(); lincon X1 ne 1, X1 ne 2, X2 ne 1, X2 ne 2, X3 ne 3, X3 ne 4, X4 ne 3, X4 ne 4, X5 ne 5, X5 ne 6, X6 ne 5, X6 ne 6; run;By using PROC OPTMODEL in SAS/OR, you can find both an 8-year schedule with no repeats (version 1) and a 6-year schedule with no repeats and with each couple giving to each of the comb(4,2) = 6 other pairs exactly once (version 2). The code is attached.
The couples are {1,2}, {3,4}, and {5,6}.
For version 1, PROC OPTMODEL yields:
For version 2, PROC OPTMODEL yields:
This is exactly what I need!!! We are a family of 10, including parents, siblings, and siblings' spouses. Spouses don't give to each other and of course you don't give to yourself! For the life of me, I can't figure out how to do it. I'm NOT a statistical programmer and need help! I'll send you some cookies this Christmas if you can create my family's gift exchange grid!!
Dear Debbie,
Merry Christmas: http://blogs.sas.com/content/iml/2011/11/15/the-great-christmas-gift-exchange-revisited/
Rick
Pingback: Secret Santa: What is the probability of pulling your own name from a hat? - The DO Loop
Pingback: The great Christmas gift exchange revisited - The DO Loop
Thank you! This was just what I was looking for. We have ben doing this with familys. But recently are family has explosed with newly married couples. The flaw was that every year they call to say, who has who? We decided to divide into 2 groups, adults 18 and up and youth 0-17. I can implement this and the work is done for up coming years! With sincere appreciation.
Wow! This may be just what I need! My brother created a randomizer for one year, but doesn't know how to set it up so certain people won't get each other and so you won't have duplicates in future years. Will your program work on LARGE groups of 50-100 with no duplicates for 8 years? Can it be made to never have duplicates until all combinations have been made (we won't live that long)? I know nothing about programming, but am trying to find a program that will remember and not duplicate past years with a preference not to have members of the same immediate family get each other. Does your program let me specify that? Thank you!
Unfortunately, I am not really set up to make customized gift exchange lists. Sorry.
Pingback: Create and use a permutation matrix in SAS - The DO Loop