The other day I was at the grocery store buying a week's worth of groceries. When the cashier, Kurt (not his real name), totaled my bill, he announced, "That'll be ninety-six dollars, even."
"Even?" I asked incredulously. "You mean no cents?"
"Yup," he replied. "It happens."
"Wow," I said, with a sly statistical grin appearing on my face, "I'll bet that only happens once in a hundred customers!"
Kurt shrugged, disinterested. As I left, I congratulated myself on my subtle humor, which clearly had not amused my cashier. "Get it?" I thought to myself, "One chance in a hundred? The possibilities are 00 through 99 cents."
But as I drove home, I began to wonder: maybe Kurt knows more about grocery bills than I do. I quickly calculated that if Kurt works eight-hour shifts, he probably processes about 100 transactions every day. Does he see one whole-dollar amount every shift, on average? I thought back to my weekly visits to the grocery store over the past two years. I didn't recall another whole-dollar amount.
So what is the probability that this event (a grocery bill that is exactly a multiple of a dollar) happens? Is it really a one-chance-in-a-hundred event, or is it rarer?
The Distribution of Prices for Grocery Items
As I started thinking about the problem, I became less confident that I knew the probability of this event. I tried to recall some theory about the distribution of a sum. "Hmmmm," I thought, "the distribution of the sum of N independent random variables is the convolution of their distributions, so if each item is uniformly distributed...."
I almost got into an accident when the next thought popped into my head: grocery prices are not uniformly distributed!
I rushed home and left the milk to spoil on the counter while I hunted for old grocery bills. I found three and set about analyzing the distribution of prices for items that I buy at my grocery store. (If you'd like to do your own analysis, you can download the SAS DATA step program .)First, I used SAS/IML Studio to create a histogram of the last two digits (the cents) for items I bought. As expected, the distribution is not uniform. More than 20% of the items have 99 cents as part of the price. Almost 10% were "dollar specials."
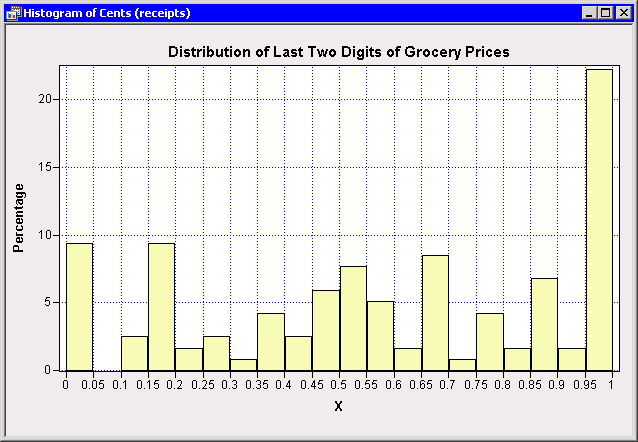
Frequent values for the last two digits are shown in the following PROC FREQ output:
Last2 Frequency Percent ------------------------------ 0.99 24 20.51 0.00 10 8.55 0.19 7 5.98 0.49 7 5.98 0.69 7 5.98 0.50 6 5.13 0.89 6 5.13 |
The distribution of digits would be even more skewed except for the fact that I buy a lot of vegetables, which are priced by the pound.
Hurray for Sales Tax!
Next I wondered whether sales tax affects the chances that my grocery bill is an whole-dollar amount. A sales tax of S results in a total bill that is higher than the cost of the individual items:
Total = (1 + S) * (Cost of Items)
Sales tax is good—if your goal is to get a "magic number" (that is, an whole-dollar amount) on your total grocery bill. Why? Sales tax increases the chances of getting a magic number. Look at it this way: if there is no sales tax, then the total cost of my groceries is a whole-dollar amount when the total cost of the items is $1.00, $2.00, $3.00, and so on. There is exactly $1 between each magic number. However, in Wake County, NC, we have a 7.75% sales tax. My post-tax total will be a whole-dollar amount if the total pre-tax cost of my groceries is $0.93, $1.86, $2.78, $3.71, and so on. These pre-tax numbers are only 92 or 93 cents apart and therefore happen more frequently than if there were no sales tax. With sales tax rates at a record high in the US, I wonder if other shoppers are seeing more whole-dollar grocery bills?
This suggests that my chances might not be one in 100, but might be as high as one in 93—assuming that the last digits of my pre-tax costs are uniformly distributed. But are they? There is still the nagging fact that grocery items tend to be priced non-uniformly at values such as $1.99 and $1.49.
Simulating My Grocery Bill
There is a computational way to estimate the odds: I can resample from the data and simulate a bunch of grocery bills to estimate how often the post-tax bill is a whole-dollar amount. Since this post is getting a little long, I'll report the results of the simulation next week. If you are impatient, why not try it yourself?
Here is a link to the follow-up article that uses bootstrapping to estimate the probability.


8 Comments
This actually happened to me today, and I had remembered seeing the title of this blog entry. So, I came straight back to my desk to read the contents! This has happened to me before, but it does always seem very odd.
In elementary school, we actually had a math class contest to see what team could get their grocery bill closest to a certain even dollar amount. My team was the only one who ever got a bill right on the dot.
I will be anxious to hear what your results are next week!
Did you ever finish the computation? Today I got one bill for $8.00 and one for $25.00 at the same store!
Yes, the "Trackback" above links to the statistical analysis.
Pingback: Resampling and simulating my grocery bills - The DO Loop
Pingback: Readers’ choice 2010: The DO Loop’s most-read posts - The DO Loop
hy Rick,
can you show me an example in iml code of convolution for aggregate loss (frequency * severity) by FFT and IFFT?
tnx,
Nico
If you google "sas iml convolution," the first hit is http://support.sas.com/documentation/cdl/en/imlug/59656/HTML/default/viewer.htm#langref_sect138.htm
yes, i dont know, math was never my strong suit but the idea of 1 in 100 chance has popped up before of getting to a whole number and i think i will stick with that lol. In the end its both to difficult and time consuming to do such conversions and the like myself. Good thing their is google and forums though XD.