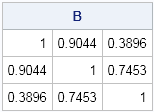
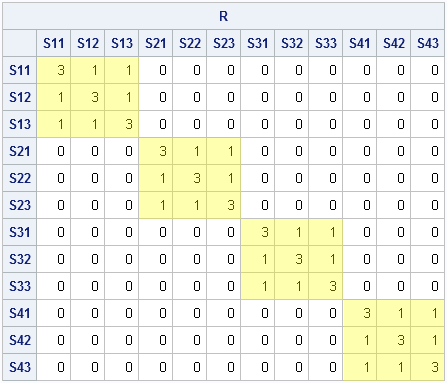
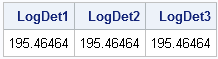
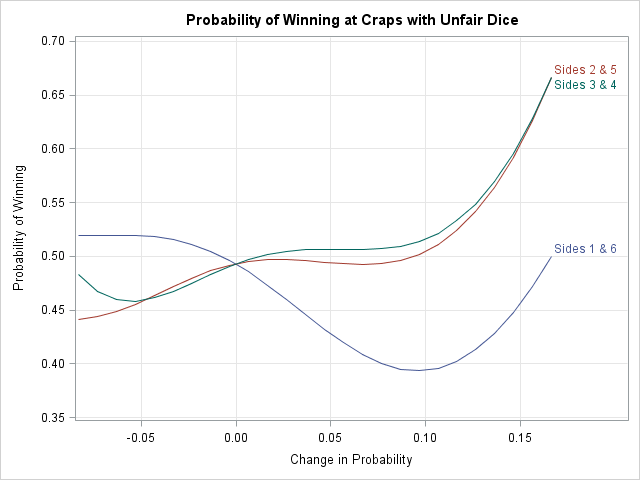
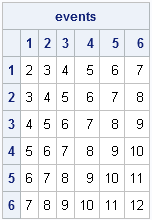
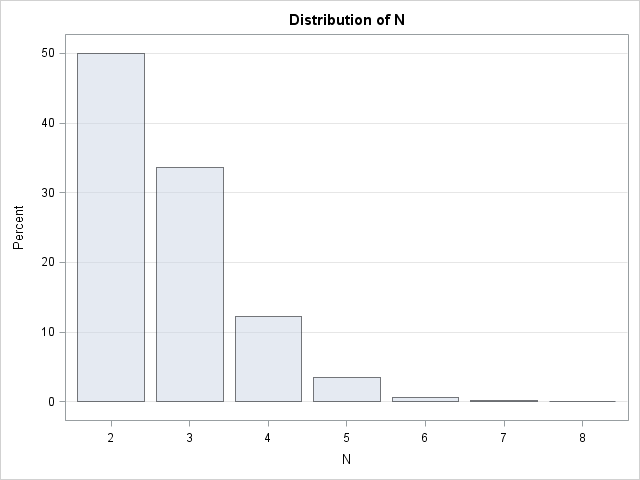
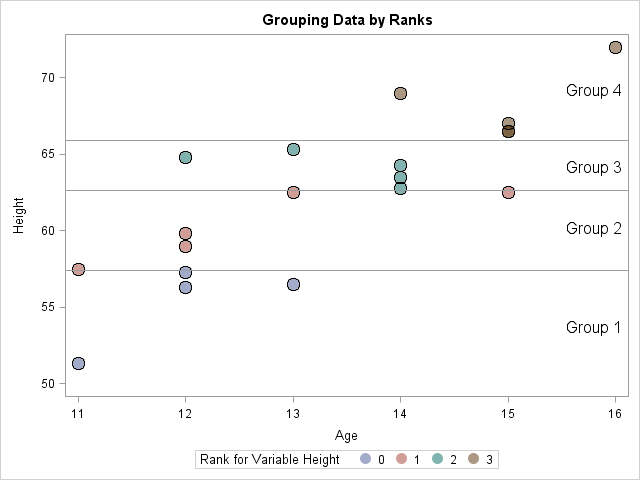
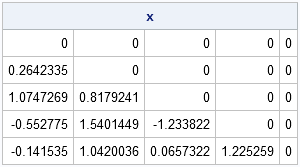
A while ago I saw a blog post on how to simulate Bernoulli outcomes when the probability of generating a 1 (success) varies from observation to observation. I've done this often in SAS, both in the DATA step and in the SAS/IML language. For example, when simulating data that satisfied