Rick Wicklin, PhD, is a distinguished researcher in computational statistics at SAS and is a principal developer of SAS/IML software. His areas of expertise include computational statistics, simulation, statistical graphics, and modern methods in statistical data analysis. Rick is author of the books Statistical Programming with SAS/IML Software and Simulating Data with SAS.
When a categorical variable has dozens or hundreds of categories, it is often impractical and undesirable to create a bar chart that shows the counts for all categories. Two alternatives are popular: Display only the Top 10 or Top 20 categories. As I showed last week, to do this in
Sometimes a categorical variable has many levels, but you are only interested in displaying the levels that occur most frequently. For example, if you are interested in the number of times that a song was purchased on iTunes during the past week, you probably don't want a bar chart with
I am pleased to announce that this year at SAS Global Forum 2013 (San Francisco, April 27 to May 1, 2013) I am giving a free hands-on workshop (HOW) entitled "Getting Started with the SAS/IML Language." If you are not familiar with the very popular Hands-On Workshop series at SAS
It's the start of a new year. Have you made a resolution to be a better data analyst? A better SAS statistical programmer? To learn more about multivariate statistics? What better way to start the New Year than to read (or re-read!) the top 12 articles for statistical programmers from
In my previous post, I described how to implement an iterated function system (IFS) in the SAS/IML language to draw fractals. I used the famous Barnsley fern example to illustrate the technique. At the end of the article I issued a challenge: can you construct an IFS whose fractal attractor
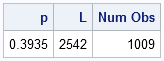
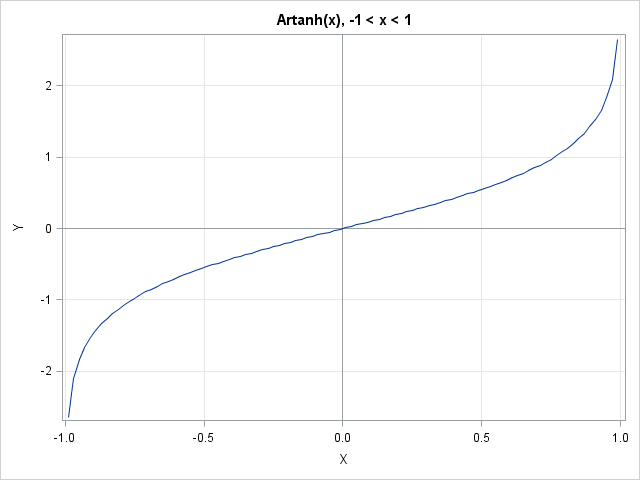
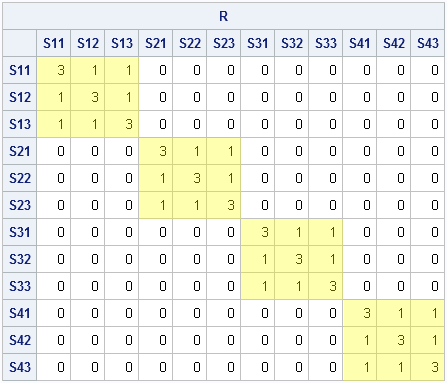
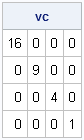
Fractals. If you grew up in the 1980s or '90s and were interested in math and computers, chances are you played with computer generation of fractals. Who knows how many hours of computer time was spent computing Mandelbrot sets and Julia sets to ever-increasing resolutions? When I was a kid,
In a recent article on efficient simulation from a truncated distribution, I wrote some SAS/IML code that used the LOC function to find and exclude observations that satisfy some criterion. Some readers came up with an alternative algorithm that uses the REMOVE function instead of subscripts. I remarked in a
It seemed like an easy task. A SAS user asked me how to use the SGPLOT procedure to create a bar chart where the vertical axis shows percentages instead of counts. I assumed that there was some simple option that would change the scale of the vertical axis from counts
Frequently someone will post a question to the SAS Support Community that says something like this: I am trying to do [statistical task]and SAS issues an error and reports that my correlation matrix is not positive definite. What is going on and how can I complete [the task]? The statistical
Last week I wrote about using acceptance-rejection algorithms in vector languages to simulate data. The main point I made is that in a vector language it is efficient to generate many more variates than are needed, with the knowledge that a certain proportion will be rejected. In last week's article,
