Clip values into an interval

Years ago, I wrote an article about the "trap and cap" programming technique. The idea is that programmers should "trap" inputs to functions (like SQRT, LOG, and QUANTILE functions) to avoid domain errors. In addition, when visualizing a function's range, you should "cap" the output to improve graphs of functions (such as LOG, 1/X, or TAN) that contain singularities.

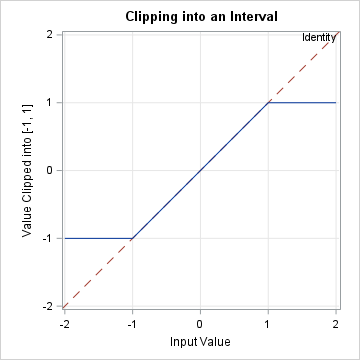
Each of these is an example of what computer scientists call clipping or clamping. Mathematicians call it truncation to an interval. An example is shown to the right. In the example, input values are in the interval [-2, 2]. The "clip" function ensures that the values are clipped into the interval [-1, 1]. For references, the identity function is shown as a dashed line in the background.

This article shows how to write SAS logic for clipping values in the DATA step and in SAS IML.

Clipping in the DATA step: Nested MAX and MIN functions

In the DATA step, the most straightforward way to truncate a value x to the interval [a, b] is to use nested calls to the MIN and MAX functions. First, take the minimum between the value and the upper bound, b. This value is less than or equal to b. Then take the maximum of the lower bound, a, and the previous result. The result is greater than or equal to a.

You can define a simple macro to encapsulate this logic:

/* clip a value x into the interval [low, high] */
%macro CLIP(low, value, high);
   (max(&low, min(&value, &high)))
%mend;
data ClipVals;
input x @@;
clipped = %CLIP(-1, x, 1);
datalines;
-2 -1.5 -0.5 0 0.5 1.5 2
;
 
proc print; run;

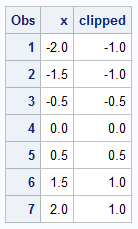
In this program, the value for x is clipped into the interval [-1, 1]. All values less than -1 become -1; all values greater than 1 become 1.

Clipping in PROC IML: Elementwise operators

If you are working with vectors or matrices in PROC IML, the previous code is probably not what you want to use. The MIN and MAX functions return a scalar value, which is the minimum or maximum element of the vector or matrix argument. Instead, you probably want to truncate every element of a vector by using the elementwise minimum and maximum operators. If x and y are conformal quantities (for example, vectors of the same size or a scalar and a vector), then you can use the elementwise operators, as follows:

The elementwise maximum is x <> y.
The elementwise minimum is x >< y.

You can encapsulate this logic by defining a SAS IML function that clips elements of a vector, x, into an interval [a,b]. The interval is represented as a two-element vector.

/* use the elementwise minimum (><) and elementwise maximum (<>) operators to 
   truncate elements of a vector into an interval. */
proc iml;
start Clip(x, ab);
   a = ab[1]; b = ab[2];
   return( a <> (x >< b) );
finish;
 
x = {-2, -1.5, -0.5, 0, 0.5, 1.5, 2};
clipped = Clip(x, {-1, 1});   /* truncate elements of x into [-1, 1] */
print x clipped;

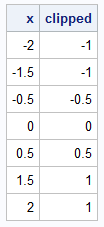
The result is the same as for the DATA step example. The elementwise operators prevent you from having to loop over elements of the vector.

What happens with missing values?

A missing value is not a mathematical number, so the clipping operation is not defined for missing values. SAS obeys certain conventions when a missing value is used in a MIN or MAX function, or is part of an elementwise operation in IML. As written, the DATA step function will return the lower limit if the value is missing. The IML function will return the upper limit. With a little additional logic, you can determine what you want to happen by using the IFN function in the DATA step and the CHOOSE function in IML. For example, if you decide that you want the clipping function to output a missing value when the input is missing, you can rewrite the body of the macro and the function as follows:

DATA step: ifn(missing(&value), ., max(&low, min(&value, &high)))
PROC IML: choose(x=., ., a (x >< b))

Summary

This article shows how to clip (or truncate) values into an interval. This technique is useful for avoiding domain errors in arguments to functions that have a restricted domain. Even for functions that are defined everywhere, such as the EXP function, you can use the clipping trick to avoid numerical underflow and overflow in your programs.

Blogs