At a conference last week, a presenter showed SAS statements that compute the logarithm of a probability density function (PDF). The log-PDF is a a common computation because it occurs when maximizing the log-likelihood function.

The presenter computed the expression in SAS by using an expression that looked like
y = LOG(PDF("distribution", x, params));
In other words, he computed the PDF and then transformed the density by applying the LOG function.

There is a better way. It is more efficient and more accurate to use the LOGPDF function to compute the log-PDF directly.

Log-transformed distributions

SAS provides several functions for computing with log-transformed distributions. In addition to the LOGPDF function, you can use the LOGCDF function to compute probabilities for the log-distribution.

Let's use the gamma distribution to see why the LOGPDF function is usually more efficient. The gamma density function with unit scale parameter is given by
f(x; a) = x^a-1 exp(-x) / Γ(a)
where Γ(a) is the value of the gamma function evaluated at a.

The log-transform of the gamma density is
log(f(x; a)) = (a-1)log(x) – x – log(Γ(a))
This formula, which is used when you compute LOGPDF("gamma", x, 2), is cheap to evaluate and does not suffer from numerical underflow when x is large. In particular, recall that in double-precision arithmetic, exp(-x) underflows if x > 709.78, so the PDF function cannot support extremely large values of x. In contrast, the formula for the log-PDF does not experience any numerical problems when x is large. The log-PDF function is also very fast to compute.

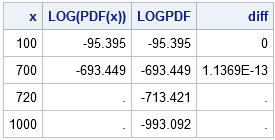
The following DATA step illustrates how to use the LOGPDF function to compute the log-gamma density. It computes the log-gamma PDF two ways: by using the LOGPDF function and by using the log-transform of the gamma PDF. The results show that the numerical values are nearly the same, but that the PDF function fails for large values of x:

data LogPDF(drop=a);
a = 2;
do x = 100, 700, 720, 1000;
   LogOfPDF = log( pdf("Gamma", x, a) ); 
   LOGPDF = logpdf("Gamma", x, a);        /* faster and more accurate */
   diff = LOGPDF - LogOfPDF;
   output;
end;
label LOGOfPDF = "LOG(PDF(x))";
run;
 
proc print noobs label; run;

By the way, SAS provides other functions that are optimized for computing the log-transformation of several well known funcions and quantities:

• The LOGBETA function computes the logarithm of the beta function. You should use logbeta(a,b) instead of log(beta(a,b)).
• The LGAMMA function computes the logarithm of the gamma function. You should use lgamma(a) instead of log(gamma(a)).
• The LCOMB function computes the logarithm of the number of combinations of n objects taken k at a time. You should use lcomb(n,k) instead of log(comb(n,k)).
• The LFACT function computes the quantity log(n!) for specified values of n. You should use lfact(n) instead of log(fact(n)).

In general, when software provides a function for directly computing the logarithm of a quantity, you should use it. The special-purpose function is typically faster, more accurate, and will handle arguments that are beyond the domain of the non-specialized function.