If you use a word three times, it's yours.
-Unknown

When I was a child, my mother used to encourage me to increase my vocabulary by saying, "If you use a word three times, it's yours for life." I believe that the same saying holds for programming techniques: Use a technique three times, and it sticks with you.

I've blogged before about various ways to fill or extract portions of a matrix. I recently used the ROW/COL technique for the third time, and I suspect I will use it more in the future. The technique (which is explained in a previous post) uses two helper functions, ROW and COL, to fill and extract certain elements in a matrix, such as the upper or lower triangular elements. The ROW and COL functions are new in SAS/IML 13.1, which is shipped with SAS 9.4m1. For example, the following statements fill the lower triangular portion of a matrix with random variates from a standard normal distribution:

proc iml;
/* Prior to SAS/IML 13.1, define helper functions ROW and COL.
   These functions are built-ins for SAS/IML 13.1 and later.  */
start row(x);  /* return matrix m such that m[i,j] = i */
   return( repeat( T(1:nrow(x)), 1, ncol(x) ));
finish;
start col(x);  /* return matrix m such that m[i,j] = j */
   return( repeat(1:ncol(x), nrow(x)) );
finish;
 
p = 5;           /* specify dimensions */
x = j(p, p, 0);  /* allocate p x p matrix of zeros */
r = row(x);      /* create helper matrices */
c = col(x);
 
/* fill lower triangle with normal variates */
lowerIdx = loc(r > c);
call randseed(12345);
y = j(1, ncol(lowerIdx));   /* allocate vector with correct number of elements */
call randgen(y, "Normal");  /* fill it with random variates */
x[lowerIdx] = y;            /* assign values to lower triangular matrix */
print x;

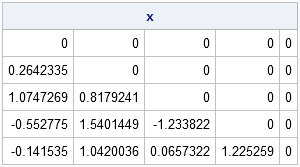
Filling the lower-triangular portion of a matrix with random numbers is not just an example that demonstrates this technique, it is also the first step in the simulation of variates from a Wishart distribution.

You can use the r and c matrices to define the indices for other portions of a matrix. For example:

• The upper triangular portion of a matrix: r < c
• the diagonal: r = c
• the anti-diagonal: r + c -1 = p
• the super- and subdiagonals, and so forth.

Try it out. And if you use it three times, it's yours for life!