I recently returned from a five-day conference in Las Vegas. On the way there, I finally had time to read a classic statistical paper: Bayer and Diaconis (1992) describes how many shuffles are needed to randomize a deck of cards. Their famous result that it takes seven shuffles to randomize a 52-card deck is known as "the bane of bridge players" because the result motivated many bridge clubs to switch from hand shuffling to computer-generated shuffling. Casual bridge players also blame this result for "slowing down the game" while the cards are shuffled more times than seems intuitively necessary.
In the second paragraph of the paper, Bayer and Diaconis introduce a "mathematically precise model of shuffling," which is known as the Gilbert-Shannon-Reeds (GSR) model. This model is known to be a "good description of the way real people shuffle real cards." (See Diaconis (1988) and the references at the end of this article.) This article describes how to implement GSR shuffling model in SAS/IML software.
The Riffle Shuffle
Computationally, you can shuffle a deck by generating a permutation of the set 1:n, but that is not how real cards are shuffled.
The riffle (or "dovetail") shuffle is the most common shuffling algorithm. A deck of n cards is split into two parts and the two stacks are interleaved. The GSR algorithm simulates this physical process.
The GSR model splits the deck into two pieces according to the binomial distribution. Each piece has roughly n/2 cards. Then cards are dropped from the two stacks according to the number of cards remaining in each stack. Specifically, if there are NL cards in the left stack and NR cards in the right stack, then the probability of the next card dropping from the right stack is NR / (NR + NL).
The following SAS/IML module is a straightforward implementation of the GSR algorithm:
proc iml;
/** Gilbert-Shannon-Reeds statistical
model of a riffle shuffle. Described in
Bayer and Diaconis (1992) **/
start GSRShuffle(deck);
n = nrow(deck);
/** cut into two stacks **/
nL = rand("Binomial", 0.5, n);
nR = n - nL;
/** left stack, right stack **/
L = deck[1:nL]; R = deck[nL+1:n];
j = 1; k = 1; /** card counters **/
shuffle = j(n,1); /** allocate **/
do i = 1 to n;
c = rand("Bernoulli", nR/(nL+nR));
if c=0 then do; /** drop from left **/
shuffle[i] = L[j];
nL = nL-1; j=j+1; /** update left **/
end;
else do; /** drop from right **/
shuffle[i] = R[k];
nR = nR-1; k=k+1; /** update right **/
end;
end;
return(shuffle);
finish; |
Testing the GSR Algorithm
You can test the algorithm by starting with a deck of cards in a known order and observing how the cards are mixed by consecutive riffle shuffles. The following statements riffle the cards seven times and store the results of each shuffle. To save space, a 20-card deck is used. The original order of the cards is denoted 1, 2, 3, ..., 20.
call randseed(1234); n = 20; /** n=52 for a standard deck **/ deck = T(1:n); s = j(n, 8); /** allocate for 8 decks **/ s[,1] = deck; /** original order **/ do i = 1 to 7; s[,i+1] = GSRShuffle( s[,i] ); end; names = "s0":"s7"; print s[colname=names]; |
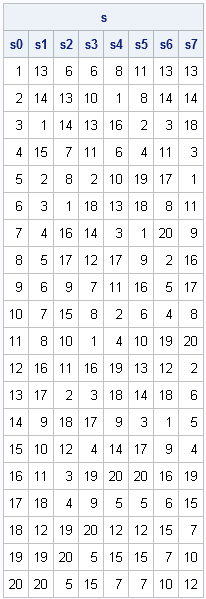
It is interesting to study the evolution of mixing the cards:
- For the first shuffle, the original deck is cut into two stacks (1:11 and 12:20) and riffled to form the second column. Notice that usually one or two cards are dropped from each stack, although at one point three cards (7, 8, 9) are dropped from the left stack.
- The second cut occurs at card 14, which is the eighth card in the second column. After the second riffle, notice that the cards 7, 8, and 9 are still consecutive, and the first and last cards are still in their original locations. Six cards (30%) are still in their initial positions in the deck.
- The pair 7 and 8 is not separated until the fourth shuffle.
- The last card (20) does not move from the bottom of the deck until the fifth shuffle.
- The first card (1) does not move from the top of the deck until the sixth shuffle.
The Efficiency of the GSR Algorithm
As far as efficiency goes, the GSRShuffle module that I've implemented here is not very efficient. As I've said before, the SAS/IML language is a vector language, so statements that operate on a few long vectors run much faster than equivalent statements that involve many scalar quantities.
This implementation of the shuffling algorithm is not vectorized. Unfortunately, because the probability of a card dropping from the left stack changes at every iteration, there is no way to call the RANDGEN function once and have it return all n numbers required to simulate a single riffle shuffle.
Or is there? Perhaps there is an equivalent algorithm that can be vectorized? Next week I'll present a more efficient version of the GSR algorithm that does not require an explicit loop over the number of cards in the deck.
References
- D. Bayer and P. Diaconis (1992), "Trailing the Dovetail Shuffle to Its Lair", Annals of Applied Probablity 2(2) 294-313
- P. Diaconis (1988), Group Representations in Probability and Statistics. IMS, Hayward, CA.
- E. Gilbert (1955) "Theory of Shuffling," Technical memorandum. Bell Laboratories.
- J. Reeds (1981), Unpublished manuscript.


4 Comments
The Interactive Matrix Language, which is the language of PROC IML, is not a "vector" language in R's sense. It is rather a "Matrix" language, since (1) the name says so; and (2) the fundamental (data) object in the language is not a vector (or 1 dim matrix), but a two-dimentional matrix. (see the "Defining a Matrix" section under "Understanding the Interactive Matrix Language" chapter of the SAS/IML User's Guide.
I'm not sure what point you're attempting to make. The SAS/IML language is a language in which you can pass matrices (which includes vectors) to functions and get back similar quantities. You can manipulate these matrices with Level 3 and Level 2 BLAS. This basic paradigm of dealing with high-level quantities(matrices and vectors) rather than scalar quantities is what makes languages such as SAS/IML, MATLAB, and R convenient languages for statistical programming and for developing algorithms.
Pingback: An improved simulation of card shuffling - The DO Loop
Pingback: Readers’ choice 2011: The DO Loop’s 10 most popular posts - The DO Loop