In a previous post, I discussed computing regression coefficients in different polynomial bases and showed how the coefficients change when you change the basis functions. In particular, I showed how to convert the coefficients computed in one basis to coefficients computed with respect to a different basis.
It turns out that there is one set of polynomial basis functions for which the regression coefficients are particularly easy to compute. They are called orthogonal polynomials, and you can compute them in SAS/IML software by using the ORPOL function. The design matrix that is returned by the ORPOL function is orthonormal, which means that each column of the matrix is orthogonal to every other column and is standardized to have unit standard deviation.
Orthogonal Polynomials
Given a set of points, x, you can evaluate the orthogonal polynomials at x by using the following statements:
proc iml; x = T(do(-1, 1, 0.2)); B3 = orpol(x, 3); /** design matrix of orthogonal polynomials **/ |
You can verify that the columns are orthonormal by computing the matrix of crossproducts:
Q = B3` * B3; /** verify B3` * B3 = I **/ reset fuzz; /** print tiny numbers as zeros **/ print Q; |
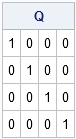
This result is important because it means that the normal equations for polynomial regression are greatly simplified when you use the B3 basis. In general, you can compute the regression coefficients for any design matrix by using the normal equations. However, because the columns of B3 are orthonormal, the first term in the normal equations is simply the identity matrix! Therefore, the normal equations simplify, as shown in the following statements:
y = {6,8,8,7,5,3,2,1,3,6,10};
/** compute parameter estimates by solving normal equations **/
/** c3 = inv(B3` * B3) * (B3` * y); **/
/** = I * (B3` * y); **/
c3 = B3` * y; /** parameter estimates (orthogonormal data matrix) **/
print c3; |
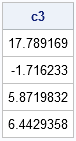
Can it really be so simple? Yes. By using the orthogonal basis functions from the ORPOL function, linear regression simplifies to a single matrix multiplication.
Interpreting the Coefficients by Changing Bases
The regression coefficients computed in the basis of orthogonal polynomials are not easy to interpret, so you might be interested in converting them to the standard basis of monomials, (1, x, x2, x3).
You could try to write down the transition matrix, as used in my previous post, but it is not trivial to write the orthogonal polynomials used to construct the B3 matrix in terms of the standard monomials. Instead, you can use a trick suggested by one of my SAS colleagues who noted that the predicted values for the orthogonal basis are the same as the predicted valued in any other basis. (The predicted values are obtained by the formula p = B3 * c1.) That means that if c1 are the regression coefficients computed in the standard monomial basis and c3 are the regression coefficients computed in the basis of orthogonal polynomials, then you can equate the predicted values:
B1 * c1 = B3 * c3
Because B3 is orthonormal, multiply both sides by the transpose of B3, which simplifies the right-hand side:
B3` * B1 * c1 = c3
This leads to the following SAS/IML statements that compute the regression coefficients with respect to the standard monomial basis in terms of the c3 coefficients that were computed previously:
/** define standard polynomial basis **/ Intercept = j(nrow(x), 1, 1); B1 = Intercept || x || x##2 || x##3; c1 = inv(B3` * B1) * c3; /** compute standard regression coefficients **/ print c1; |
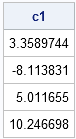
Sure enough, if you look back at my previous post, you will see that these are regression coefficients for the data in the standard polynomial basis.

5 Comments
Hi Rick,
I am fitting a linear regression model where I would like to obtain standardized regression coefficients, but some terms in the model have piece-wise linear splines. Do you have any recommendation on how to proceed: should we standardize the variable then create the splines or treat the two splines as two different terms in the model and standardize each separately?
Thanks
Hocine
Generate the spline effects, then use PROC STDIZE to standardize. Each PL spline is its own effect. See "Visualize a regression with splines."
Dr. Wicklin:
I am using ORPOL to compute linear and quadratic contrast coefficients to use in PROC Mixed to evaluate treatment responses. I'm applying them to a small test data set with 3 treatments, and 4 observations per treatment. Treatments are unequally spaced levels (0, 120, 480), and the middle treatment (120) has one missing value. I'm using ORPOL as follows:
x1={0 120 480};
w={4 3 4};
x1p=orpol(x1,2,w);
When I apply the weighted coefficients that come directly from the x1p matrix for the linear and quadratic contrasts in Proc Mixed, the contrasts are non-estimable. If I don't weight for missing values, the contrasts are estimable. I noticed that the weighted contrasts don't sum to zero, which I assume is the reason for the non-estimable error. To get the contrasts to sum to zero, I multiplied each coefficient by its respective weight. When I used those adjusted coefficients in Proc Mixed, the contrasts are estimable. Is this the correct approach to fixing the error with the contrasts?
Thanks,
Mike Galyean
I don't know the answer your question.
It does concern me that you are using three points for a quadratic model. The model (which has three parameters) will fit exactly with no errors. I suspect this might be related to the non-estimable quantities.
I suggest you post your PROC MIXED code to the SAS Support Communities and ask your question there.
Thanks. The 3 treatments example was just for a quick test. I've also had the same problem with a 4 x 4 Latin square. I'll post the code for the 4 x 4 Latin square to the SAS Support Communities and see if anyone has encountered a similar problem.