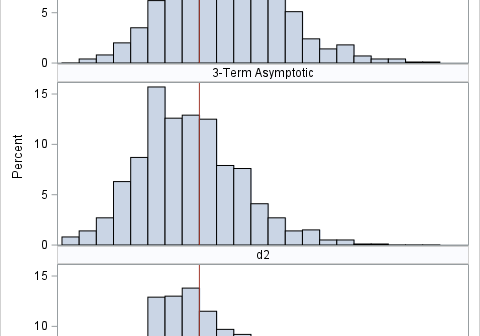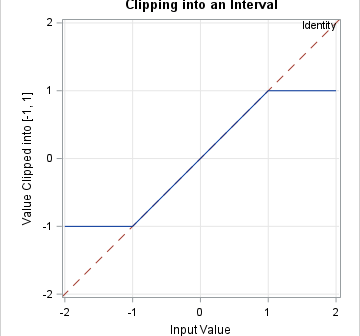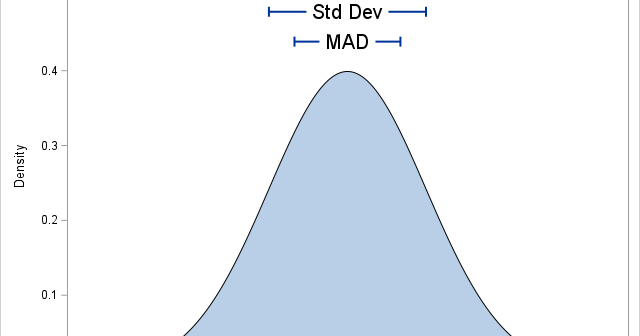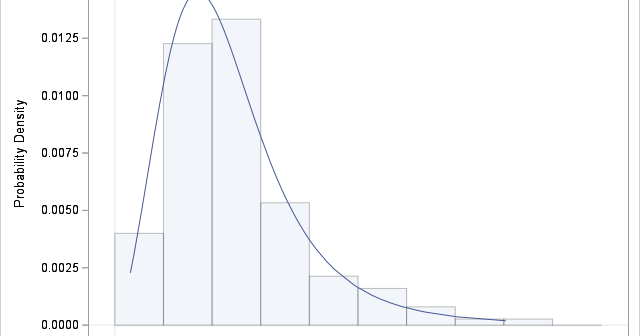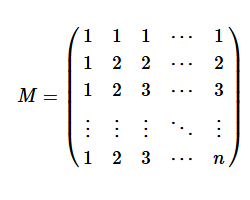
When you implement a numerical algorithm, it is helpful to write tests for which the answer is known analytically. Because I work in computational statistics, I am always looking for test matrices that are symmetric and positive definite because those matrices can be used as covariance matrices. I have previously