A palindrome is a sequence of letters that is the same when read forward and backward. In brief, if you reverse the sequence of letters, the word is unchanged. For example, 'mom' and 'racecar' are palindromes. You can extend the definition to phrases by removing all spaces and punctuation marks from the phrase and asking whether the remaining letters are a palindrome. For example, 'borrow or rob?' is a palindrome because the sequence of letters 'borroworrob' is the same when read forward and backward.

Recently, I saw a new kind of palindrome: The rotational palindrome. You take a word (written in lowercase) and rotate it 180 degrees so that the letters are upside down and reversed. You then ask whether the pattern of letters matches the original word. If so, you have found a rotational palindrome!

This article shows how to detect palindromes, palindrome phrases, and rotational palindromes in SAS. Along the way, we learn about a few useful string-comparison functions, such as the UPCASE, STRIP, COMPRESS, REVERSE, and TRANSLATE functions.

Detect a palindrome word in SAS

To introduce the topic of palindromes, let's first consider only words. If you want to determine whether a word is a palindrome, do the following:

1. Use the UPCASE function to convert all letters to uppercase.
2. Use the REVERSE function to obtain the reversed sequence of letters.
3. Use the STRIP function to remove any leading or trailing blanks. Compare the original and the reversed sequence of letters. If the two sequences are the same, the word is a palindrome.

The following SAS DATA step implements this algorithm on a series of words.

data Words;
length source $120;
input source;
datalines;
solos
Hannah
Dad
madaM
racecar
SAS
STATs
programmer
;
 
/* detect palindrome words */
data Palindrome;
  set Words;
  length str reverse $120;
  str = upcase(source);
  reverse = reverse(str);
  isPalindrome = (strip(str) = strip(reverse));  /* 0/1 indicator variable */
run; 
 
proc print noobs; run;

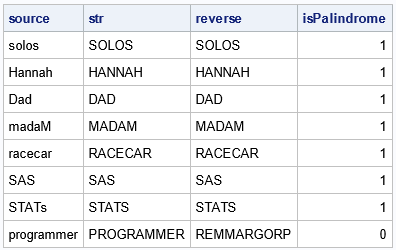
The data set contains an indicator variable (isPalindrome), which has the value 1 for palindrome words and the value 0 if the word is not a palindrome. Words like 'solos', 'dad', and 'SAS' are palindromes. The word 'programmer' is not.

Detect a palindrome phrase in SAS

The same logic works for a palindromic phrase but requires an extra step. For a phrase, you must first remove blanks and punctuation from the string, then apply the preceding logic to the remaining sequence of letters. You can use the COMPRESS function in SAS to remove blanks and punctuation. Often, programmers call the COMPRESS function with two arguments: the input string and a set of characters to remove from the string. However, the optional third argument provides a way to remove common sets of characters from the input string. For example, to remove all punctuation characters, you can specify 'p' as part of the third argument. To remove all whitespace, you can specify the 's' modifier. You can specify 'ps' to combine those two modifiers, as done below:

data Sentences;
length source $120;
infile datalines truncover;
input source $ 1-120;
/* use DATALINES4 if a string includes a semicolon */
datalines;   
Madam, I'm Adam.
Step on no pets.
No lemon, no melon.
To be or not to be.
My gym, sir, is my gym.
Was it a cat I saw?
A man, a plan, a canal: Panama!
racecar
SAS
programmer
;
 
/* detect palindrome phrases (also works for words) */               
data Palindrome;
  set sentences;
  length str reverse $120;
  str = compress(upcase(source), , 'ps');  /* remove punctuation and whitespace */
  reverse = reverse(str);
  palindrome = (str = strip(reverse));     /* no blanks in str */
  drop reverse;
run; 
 
proc print  noobs; run;

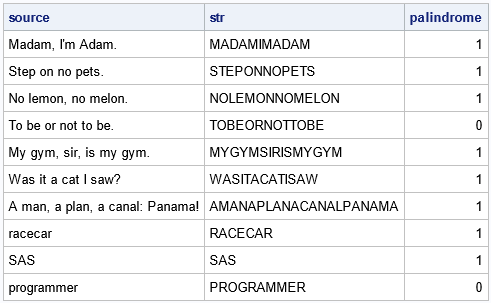
This program handles words as well as phrases, so it can replace the program in the previous section. As a boy, I encountered the palindromic phrase "A man, a plan, a canal: Panama!" in a book of word games; it has always amused me!

Generalizations of palindromes

The traditional palindrome is a specific example of a more general mathematical problem. Mathematically, a transformation is a function that maps a set into itself. A fixed point is an element in the domain of a transformation that is mapped to itself. If R is the transformation on a set of letters that reverses the letters, then a palindrome is a fixed point for the R transformation.

With this generalization, you can play all sorts of mathematical games. You can search for the closest palindrome to a given word. You can search for "near palindromes." For example, 'bevel' is a near palindrome because you can replace the 'b' with an 'l' to obtain the palindrome 'level'.

Alternatively, you can change the transformation and find fixed points of the new transformation. This is the idea behind a rotational palindrome. Certain lowercase letters look like a letter when you rotate them by 180 degrees. I use the phrase rotationally similar to refer to a pair of letters like 'b' and 'q' that are 180-degree rotations of each other. Some letters (such as 'o' and 's') are rotationally similar to themselves. Given a set of letters, define a transformation in two steps: first map certain letters to their rotationally similar image. Next, apply the REVERSE transformation. You then search for fixed points of the composite mapping.

Each of the following 13 lowercase letters is rotationally similar to another lowercase letter. Five of them ('l', 'o', 's', 'x', and 'z') are self-similar:

b -> q
d -> p
l -> l
m -> w
n -> u
o -> o
p -> d
q -> b
s -> s
u -> n
w -> m
x -> x
z -> z

To completely define the transformation, you should also define how it acts on the remaining letters ('a', 'c', 'e', etc.). Words that contain these letters are never rotational palindromes because rotating these letters by 180 degrees does not result in a valid lowercase letter.

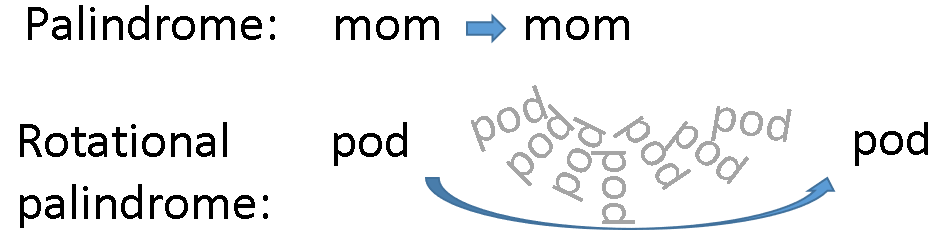
For example, 'mom' is not a rotational palindrome because if you rotate it 180 degrees you get 'wow'. But 'pod' is a rotational palindrome because the letter 'p' is the 180-degree rotation of 'd' (and vice versa) and the letter 'o' is rotationally symmetric. The word 'mow' is a rotational palindrome, but 'maw' is not because the letter 'a' is not rotationally similar to any other letter.

Rotational palindromes in SAS

You can use the TRANSLATE function in SAS to define the rotational transformation. The TRANSLATE function takes three arguments: the input string and two replacement strings, TO and FROM. The FROM string is the set of letters that you want to replace, and the TO string is the set of letters that you want to use for the replacement. I think it is clearest to define a string that has 26 letters so that you can see how every letter in a word is transformed. In the following program, the letters that do not have rotational cousins are assigned to a period (.). Assuming that you remove all punctuation from the input string, this choice will ensure that the program will correctly identify rotational palindromes.

You can use a mathematical trick to check for a rotational palindrome. A rotation by 180 degrees is mathematically equivalent to a horizontal reflection followed by a vertical reflection. Therefore, you can program a 180-degree rotation by first substituting the rotationally similar letter and then reversing the string, as follows:

data Words2;
length source $120;
infile datalines truncover;
input source $ 1-120;
datalines;
solos
mow
maw
pod
dad
mop dow
madam
SAS
;
 
/* detect rotational palindromes */
data Rotate;
  set Words2;
  length str flip flipReverse $120;
  FROM='abcdefghijklmnopqrstuvwxyz0123456789'; /* old values (including digits) */
  TO = '.q.p.......lwuodb.s.n.mx.z012...9.86'; /* new values (including digits) */
  str = compress(lowcase(source), , 'ps');     /* remove blanks and punctuation */
  flip = translate(str, TO, FROM);             /* map to rotationally similar letters */        
  flipReverse = strip(reverse(flip));          /* do the usual palindrome check */
  isRotPalindrome = (str = flipReverse);
  drop TO FROM;
run; 
 
proc print noobs; run;

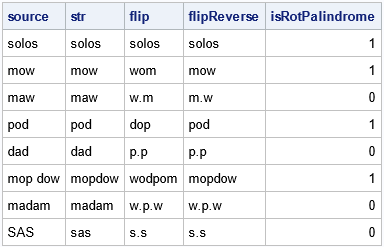
The program removes punctuation and spaces, translates each letter to its rotationally similar image, then determines whether the reversed string is equal to the original string. The program verifies that 'mow' and 'pod' are rotational palindromes. In addition, notice that the word 'solos' is a very special word. It is both a traditional palindrome and a rotational palindrome! A palindrome that contains only self-similar letters is also a rotational palindrome.

Summary

A traditional palindrome is a string of letters that are the same in forward and reversed order. This article shows how to use built-in string functions in SAS to detect palindromes. Some useful functions include UPCASE, STRIP, COMPRESS, and REVERSE. In addition, you can generalize the notion of a palindrome. A generalized palindrome is a fixed point for a transformation of the letters in a string. I show how to define a rotational palindrome by mapping certain letters to their rotationally similar images, then checking whether the reversal of the resulting string is equal to the original string.

Feel free to share any thoughts you might have regarding palindromes. Do you think rotational palindromes are interesting? Can you find any words that are longer than five letters and are rotational palindromes? Can you think of other interesting transformations of strings? What are the fixed points (palindromes) for those transformations?