The SAS/IML language and the MATLAB language are similar. Both provide a natural syntax for performing high-level computations on vectors and matrices, including basic linear algebra subroutines. Sometimes a SAS programmer will convert an algorithm from MATLAB into SAS/IML. Because the languages are not identical, I am sometimes asked, "what is the SAS/IML function that is equivalent to the XYZ function in MATLAB?" One function I am often asked about is the linspace function in MATLAB, which generates a row vector of n evenly spaced points in a closed interval. Although I have written about how to generate evenly spaced points in SAS/IML (and in the DATA step, too!), the name of the SAS/IML function that performs this operation (the DO function) is not very descriptive. Understandably, someone who browses the documentation might pass by the DO function without realizing that it is the function that generates a linearly spaced vector. This article shows how to construct a SAS/IML function that is equivalent to the MATLAB linspace function.

Generate equally spaced points in an interval

Syntactically, the main difference between the DO function in SAS/IML and the linspace function in MATLAB is that the third argument to the DO function is a step size (an increment), whereas the third function to the linspace function is the number of points to generate in an interval. But that's no problem: to generate n evenly spaced points on the interval [a, b], you can use a step size of (b – a)/(n – 1). Therefore, the following SAS/IML function is a drop-in replacement for the MATLAB linspace function:

proc iml;
/* generate n evenly spaced points (a linearly spaced vector) in the interval [a,b] */
start linspace(a, b, numPts=100);
   n = floor(numPts);               /* if n is not an integer, truncate */
   if n < 1 then return( {} );      /* return empty matrix */
   else if n=1 then return( b );    /* return upper endpoint */
   return( do(a, b, (b-a)/(n-1)) ); /* return n equally spaced points */
finish;

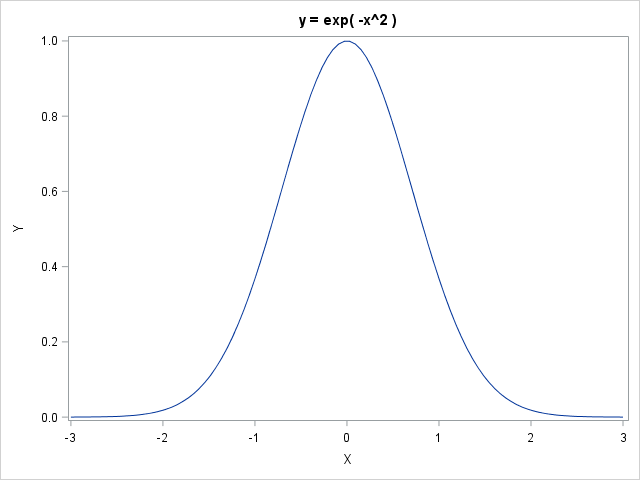
A typical use for the linspace function is to generate points in the domain of a function so that you can quickly visualize the function on an interval. For example, the following statements visualize the function exp( -x² ) on the domain [-3, 3]:

x = linspace(-3, 3);                /* by default, 100 points in [-3,3] */
title "y = exp( -x^2 )";
call series(x, exp(-x##2));         /* graph the function */

Reminder: "10.0 times 0.1 is hardly ever 1.0"

This is a good time to remind everyone of the programmer's maxim (from Kernighan and Plauger, 1974, The Elements of Programming Style) that "10.0 times 0.1 is hardly ever 1.0." Similarly, "5 times 0.2 is hardly ever 1.0." The maxim holds because many finite decimal values in base 10 have a binary representation that is infinite and repeating. For example, 0.1 and 0.2 are represented by repeating decimals in base 2. Specifically, 0.2₁₀ = 0.00110011...₂. Thus, just as 3 * (0.3333333) is not equal to 1 in base 10, so too is 5 * 0.00110011...₂ not equal to 1 in base 2.

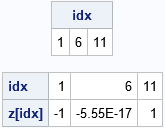
A consequence of this fact is that you should avoid testing floating-point values for equality. For example, if you generate evenly spaced points in the interval [-1, 1] with a step size of 0.2, do not expect that 0.0 is one of the points that are generated, as shown by the following statements:

z = do(-1, 1, 0.2);
/* find all points that are integers */
idx = loc( z = int(z) );               /* test for equality (bad idea) */
print (idx // z[,idx])[r={'idx', 'z[idx]'}];  /* oops! 0.0 is not there! */
 
print z;                               /* show that 0.0 is not one of the points */

When you query for all values for which z = int(z), only the values -1 and +1 are found. If you print out the values in the vector, you'll see that the middle value is an extremely tiny but nonzero value (-5.55E-17). This is not a bug but is a consequence of the fact that 0.2 is represented as a repeating value in binary.

So how can you find the points in a vector that "should be" integers (in exact arithmetic) but might be slightly different than an integer in floating-point arithmetic? The standard approach is to choose a small distance (such as 1e-12 or 1e-14) and look for floating-point numbers that are within that distance from an integer. In SAS, you can use the ROUND function or check the absolute value of the difference, as follows:

eps = 1e-12;
w = round(z, eps);                            /* Round to nearest eps */
idx = loc( int(w) = w);                       /* find points are within epsilon of integer */
print idx;                                    
 
idx = loc( abs(int(z) - z) < eps );           /* find points whose distance to integer is less than eps */
print (idx // z[,idx])[r={'idx', 'z[idx]'}];

In summary, this article shows how to define a SAS/IML function that is equivalent to the MATLAB linspace function. It also reminds us that some finite decimal values (such as 0.1 and 0.2) do not have finite binary representations. When these values are used to generate an arithmetic sequence, the resulting vector of values might be different from what you expect. A wise practice is to never test a floating-point value for equality, but instead to test whether a floating-point value is within a small distance from a target value.