My previous blog post shows how to use PROC LOGISTIC and spline effects to predict the probability that an NBA player scores from various locations on a court. The LOGISTIC procedure fits parametric models, which means that the procedure estimates parameters for every explanatory effect in the model. Spline bases enable you to fit complex models, but it is easy to generate many spline effects, which means that you need to be careful not to overfit the data.

In contrast, modern nonparametric models enable you to balance the complexity of a model with the goodness of fit, thus reducing the likelihood of overfitting the data. SAS provides several procedures that fit nonparametric regression models for a binary response variable. Options include:

• Use variable selection techniques in PROC LOGISTIC or PROC HPGENSELECT to allow the data to select the effects that best model the data. Variable selection creates a hybrid analysis that has properties of nonparametric models while preserving the interpretability of parametric models.
• Use the GAMPL procedure in SAS/STAT 14.1 (SAS 9.4m3) to fit the data. The GAMPL procedure uses penalized likelihood (PL) methods to fit generalized additive models (GAM).

Other choices in SAS/STAT software include the ADAPTIVEREG procedure, which combines splines with variable selection techniques, and the HPSPLIT procedure, which is a tree-based classification procedure. Both procedures were introduced in SAS/STAT 12.1.

Generalized additive models in SAS

Generalized additive models use spline effects to model nonlinear relationships in data. A smoothing penalty is applied to each spline term in an attempt to model nonlinear features without overfitting the data. For details and examples, you can read the GAMPL documentation or watch a video about PROC GAMPL.

The syntax for the GAMPL procedure is similar to the familiar syntax for PROC LOGISTIC or PROC GENMOD. You can specify spline effects and the distribution of the response variable. The following statement uses a two-dimensional thin-plate spline to model the probability of Stephen Curry scoring from various shooting locations. The data are from Robert Allison's blog "How to graph NBA data with SAS." You can download the complete SAS program that produces the graphs in this post.

proc gampl data=Curry;
   where Shot_Distance <= 30;
   model Shot_Made(event='Made') = Spline(X Y / maxdf=40) / dist=binary;
   id X Y Shot_Made;
   output out=GamPLOut;
run;

The OUTPUT statement saves the predicted probabilities to a data set. The option MAXDF=40 tells the procedure to consider up to 40 degrees of freedom for the spline effect and to choose the smoothing parameter that provides the best tradeoff between model complexity and goodness of fit. For the Stephen Curry data, the optimal smoothing parameter results in 14.7 degrees of freedom.

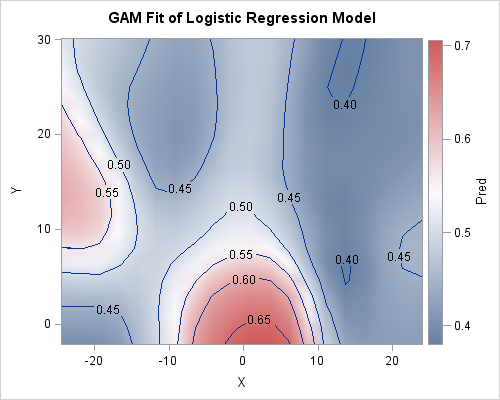
You can use the graph template language (GTL) to create a contour plot of the predicted probabilities. The contour map is qualitatively similar to the probabilities that were predicted by the PROC LOGISTIC analysis in my previous post. There is an area of high probability near the basket at (0,0). The probabilities on the right side of the graph are lower than on the left. There is a "hot spot" on the left side of the graph, which corresponds to a high probability that Curry will score from that region.

Verify: The fundamental principle of nonparametric analysis

I initially view the results of any nonparametric analyses with skepticism. I trust the mathematics behind the methods, but I need to be convinced that a qualitative feature in the predicted values is real and not merely an artifact of some complicated nonparametric witchcraft.

There are many statistical techniques that enable you to evaluate whether a model fits data well, but it is wise to perform a basic "sanity check" by using a different nonparametric procedure to analyze the same data. If the two analyses reveal the same qualitative features in the data, that is evidence that the features are truly present. Conversely, if two models produce different qualitative features, then I question whether either model is accurate. I call this sanity check the fundamental principle of nonparametric analysis: Trust, but verify.

Let's apply the fundamental principle to the NBA data by running PROC ADAPTIVEREG:

proc adaptivereg data=Curry plots;
   where Shot_Distance <= 30;
   model Shot_Made(event='Made') = X Y / dist=binary;
   output out=AdaptiveOut p(ilink);
run;

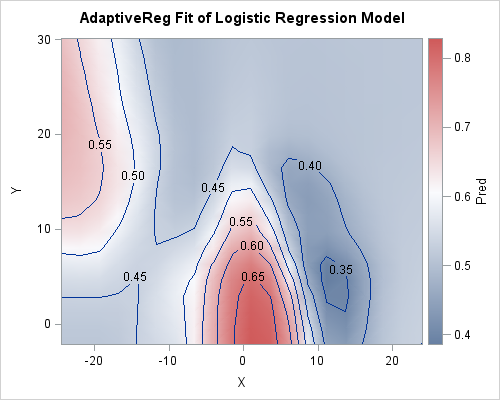
The PROC ADAPTIVEREG analysis is shown to the left. The contour plot shows the same qualitative features that were apparent from the LOGISTIC and GAMPL analyses. Namely, the probability of scoring is high under the basket, low to the right, average up the middle, and high on the left. Seeing these features appear in several analyses gives me confidence that these features of the data are real. After verifying that the models are qualitatively similar, you can investigate which model is better, perhaps by splitting the data into subsets for model training, validation, and testing.

Summary

This article briefly introduced two nonparametric procedures in SAS that can analyze binary response variables and other response distributions. The two analyses produced qualitatively similar predictions on sample data. The fundamental principle of nonparametric analysis is a meta-theorem that says that you should verify the qualitative predictions of a nonparametric model. Reproducibility is a necessary (but not sufficient) condition to believe that a feature is real and not spurious. For this example, all analyses agree that Stephen Curry shoots better from one side of the court than from the other.