In a previous blog post, I described the rules for a tic-tac-toe scratch-off lottery game and showed that it is a bad idea to generate the game tickets by using a scheme that uses equal probabilities. Instead, cells that yield large cash awards must be assigned a small probability of getting a tic-tac-toe and cells that yield small cash awards can be assigned larger probabilities.

As Mohan Srivastava, the statistician who "cracked the scratch lottery code," said:

It would be really nice if the computer could just spit out random digits. But that's not possible, since the lottery corporation needs to control the number of winning tickets.

This article describes how to construct a scratch-off game that has lots of winners of small prizes, but is still profitable for the lottery corporation (the government) because the large prizes occur infrequently.

A Cell-By-Cell Probability Model for a Scratch-Off Game

The lottery corporation wants to give away many small prizes (so that the game is fun to play) while restricting the number of large pay outs (so that the game profitable).

Recall that a ticket is a winner if a set of "lucky numbers" aligns along a row, column, or diagonal. For convenience, represent the lucky numbers by a 1 and the other numbers by a 0. The key is to assign each cell in the grid a certain probability of being a 1. For example, consider the following SAS/IML matrix of probabilities:

proc iml;
p = { 1.0  1.0  0.1,
      1.0  0.02 0.2,
      0.25 0.1  0.1 };

If you assign a 1 to a grid cell based on these probabilities, the resulting grids have the following properties:

• A 1 is always placed in the first two positions of the first column (because the chance of placing a 1 there is 100%).
• The probability of getting a winning tic-tac-toe in the first column is 0.25, the product of the probabilities in the first column. This means that one fourth of all gamers will get their $3 investment back.
• A 1 is always placed in the first two positions of the first row.
• The probability of getting a winning tic-tac-toe in the first row is 0.1. This means that one tenth of all gamers will get a $5 payout, for a net gain of $2.
• Other ways of winning the game occur much less frequently.

The probabilities are assigned to lessen the chance of paying the big cash awards. For example, the middle cell gets a lucky number only 2% of the time, so winning the game by having all 1s on a diagonal (the big $250 prize!) will not happen often.

How Much and How Often Would You Win This Game?

In order to find the expected payout (in dollars) for each combination, you can compute the products of the row, column, and diagonal probabilities and multiply those values by the corresponding payouts, as shown in the following SAS/IML statements:

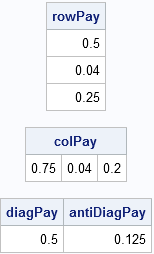
rowPay = p[,#] # {5,10,100};
colPay = p[#,] # {3 20 100};
diagPay = p[{1 5 9}][#] # 250;
antiDiagPay = p[{3 5 7}][#] #250;
print rowPay, colPay, diagPay antiDiagPay;

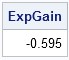
The payout for the entire game is just the sum of these individual payouts. To compute the expected gain/loss for playing the game, subtract the initial $3 purchase price:

ExpGain = -3 + sum(rowPay, colPay, diagPay, antiDiagPay);
print ExpGain;

Scratch, Scratch, Scratch: Simulating Many Games

For people more comfortable with simulation than with probability theory, you can also write a SAS/IML simulation that "plays" the game many times. The statements call the TestWinner module from my previous blog post.

NSim = 1E5;
x = j(NSim,9);
y = j(NSim,1);
/** each cell cell has different probabilities. 
    Sample 9 times. **/
do i = 1 to 9;
   call randgen(y, "BERNOULLI", p[i]);
   x[,i] = y;
end;
win = TestWinner(x);
ExpWin = win[:];
PctWin = (win>=0)[:];
print ExpWin PctWin;

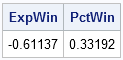
Notice that this game pays out an award 33% of the time, so it gives the players (false) hope and keeps them coming back. (Of course, for most of those "wins," you only get your money back!) The simulated result estimates that, on average, you will lose $0.58 every time you play the game. (The true expected loss is $0.595.)

Unless, of course, you know Srivastava's trick.

Choosing the Probabilities: A Better Way?

One thing bothers me about the probabilities that I chose: the probability of winning a $10 or $20 award is too small. In order to lower the chance of winning the big $250 award (getting tic-tac-toe on the diagonal), I chose a small probability for the middle cell. But this also lowers the probability of getting tic-tac-toe on the middle row and middle column.

What scheme would you use so that the chance of winning an award is a decreasing function of the size of the award?