This post is about an estimate, but not the statistical kind. It also provides yet another example in which the arithmetic mean is not the appropriate measure for a computation.

First, some background.

Last week I read a blog post by Peter Flom that reminded me that it is wrong to use an arithmetic mean to average rates. Later that day I met a man at my house to get an estimate for some work on my roof. The price of the work depends on the area of my roof. My roof has a different pitch on the front than on the back, so the calculation of area requires some trigonometry and high-school algebra. The main calculation involves finding r1 and r2 in the following diagram, which represents a cross section of my roof:

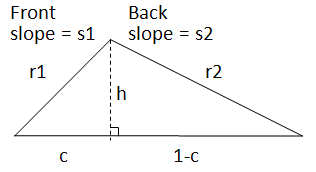
The man who was writing the estimate took a few measurements in my attic and was downstairs with his calculation in only a few minutes.

"The front of your house has a 12/12 slope," he said, using the roofer's convention of specifying a slope by giving the ratio of the number of inches that the roof rises for every twelve inches of horizontal change. "Your back roof has a 6/12 slope," he continued. "The average slope is therefore 9/12, but because I want your business I'm only going to charge you for an average slope of 8/12. I'm saving you money."

Huh? Average slopes? Peter Flom's post came to mind.

After the man left, I sharpened my pencil and put on my thinking cap. You can compute the area of roof by knowing the square footage of the attic and multiplying that value by a factor that is related to the pitch of the roof. A steeper roof means a bigger multiplication factor, and consequently costs more money. Less pitch means less money.

Hmmm, wasn't the roofing man claiming that the correct computation is to average the slopes of my roof? Isn't a slope a rate?

Using the diagram, I determined the diagonal distances r1 and r2 in terms of the slopes of my roof. The following SAS/IML module summarizes the computations:

proc iml;
/** multiplier for area of a roof, computed from two roof pitches **/
start FindRoofAreaMultiplier(pitch);
   s1 = pitch[1];     /** slope in front of house **/
   s2 = pitch[2];     /** slope in back of house **/
   c = s2/(s1+s2);    /** roof peak occurs at this proportion **/
   h = s1*s2/(s1+s2); /** roof height **/
 
   /** distances from gutters to peak of roof **/
   r1 = sqrt(c##2 + h##2);     /** along the front **/
   r2 = sqrt((1-c)##2 + h##2); /** along the back  **/
   return(r1+r2);
finish;
 
/** the two pitches of my roof **/
pitch = 12/12 || 6/12;
ExactMultiplier = FindRoofAreaMultiplier(pitch);
print ExactMultiplier;

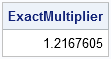
So, for my roof, the area of the roof by is 1.217 times the area of the attic. What happens if I use the average pitch to compute the multiplier?

/** average the slopes and use average in calculations **/
s = pitch[:];
pitch = s || s;
AveMultiplier = FindRoofAreaMultiplier(pitch);
print AveMultiplier;

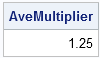
As I had suspected, using the average of the roof pitches to compute the multiplier gives an incorrect answer. This is obvious if you do the following thought experiment. Imagine that the slope of the front roof gets steeper and steeper while you hold the slope of the back roof constant. In this manner, you can make the average slope as large as you want.

In conclusion, it is not valid to use the average slope of the two roofs to estimate the area multiplier when the slopes are substantially different.

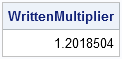
So, did the roofing man cheat me? Not really. The following computation shows that the slope of 8/12 that he used in the written estimate yields a multiplier that is slightly less than the true multiplier. The difference is about 1%, and it is in my favor:

/** pitch used in written estimate **/
s = 8/12;
pitch = s || s;
WrittenMultiplier = FindRoofAreaMultiplier(pitch);
print WrittenMultiplier;

Maybe the roofing man tells people "I'm doing you a favor" to get more business. Or, maybe he made a mistake. Or maybe he is so experienced that he just intuitively knew the correct multiplier.

In any case, statisticians know that the arithmetic mean shouldn't be used indiscriminately, and this story provides yet another example in which using the arithmetic mean leads to a wrong answer.