Last weekend was the 2016 NCAA Division I wrestling tournament. In collegiate wrestling there are ten weight classes. The top eight wrestlers in each weight class are awarded the title "All-American" to acknowledge that they are the best wrestlers in the country.

I saw a blog post on the InterMat web site that lists each All-American and the wrestler's national ranking when he was a high school senior. The data are interesting, but I wanted a simple graph that visualized the data. I decided to use SAS to create graphs that show the high school ranking for each of this year's 80 All-American wrestlers.

I was also interested in the relationship between high school ranking and placement at the NCAA tournament. Were the top NCAA wrestlers already nationally recognized while still in high school? Or were there some "late bloomers" who perfected their skills after entering college?

Ranking wrestlers

Several web sites, magazines, and organizations try to rank the top 50 or 100 US high school wrestlers in each weight class. It can be challenge to rank two individuals who have never wrestled each other. However, many of the top contenders in each weight class go to national tournaments, so there is often head-to-head data as well as data for common opponents.

An even more difficult challenge is attempting to rank the best wrestlers regardless of weight classes. How do you compare an undefeated heavyweight with an undefeated lightweight? Nevertheless, people do their best and you can find many internet lists that rank the "best pound-for-pound" wrestlers, boxers, MMA fighters, and so forth.

The high school rankings of the 2016 All-Americans

The InterMat article included whether each All-American was ranked in the Top 100 as a senior. If so, it gave the wrestler's rank. (Presumably, using their own ranking system.) If the wrestler was not nationally ranked, it lists whether he was ranked in his weight class (sort of an honorable mention), or whether he was unranked.

After importing the data into SAS, I used a custom format and PROC FREQ to tabulate the high school rankings against the wrestler's place in the NCAA tournament. You can download the data and the SAS program that generates the analyses in this article. The tabular results follow.

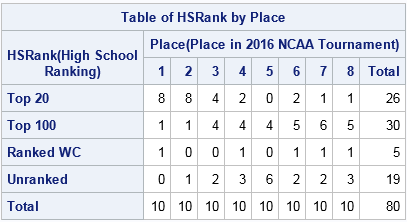
Of the wrestlers who finished first at the NCAA tournament, eight had Top 20 status as a high school senior. The results were similar for second-place finishers. However, if you look at fourth place or lower, you can see that a surprisingly large number of All-Americans who were unranked in high school. Still, with the exception of fifth place winners, more than half of each place (1–8) contained ranked wrestlers. Overall, 56 out of the 80 All-Americans were nationally ranked in high school.

PROC FREQ can automatically create a mosaic plot that graphically visualizes the tabular results. Because there are exactly ten wrestlers for each place (1–8), the mosaic plot is actually a stacked bar chart for these data. (There is an alternative way to create a stacked bar chart in SAS.)

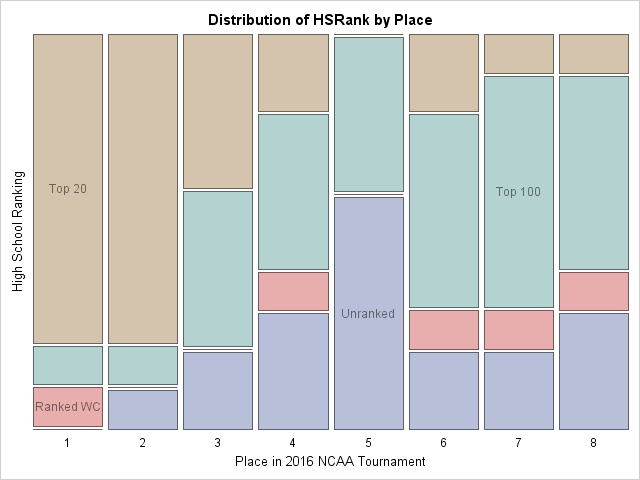
For each place, the brown rectangle represents the proportion of place winners who were ranked in the Top 20 in high school. The green rectangle represents the proportion who were not in the Top 20, but were in the Top 100. The pink rectangle shows wrestlers who were ranked in their weight classes. The blue rectangles show All-Americans who were unranked as high school seniors. Those formerly unranked wrestlers are the "late bloomers" who improved markedly and became a top college wrestler.

Association between NCAA place and high school rank

The previous graph shows that most wrestlers who placed first, second, or third were top-ranked high school wrestlers. The InterMat web site includes the exact high school ranking (1—100), so let's plot each wrestler's NCAA place against his high school ranking. To accommodate the wrestlers who were not ranked, I arbitrarily assign the rank "110" to the weight-class-ranked wrestlers. Instead of plotting the value 110 on a graph, I use the abbreviation "WC" for "weight class." I assign the rank "120" to the unranked wrestlers, and label that value by "NR" for "not ranked."

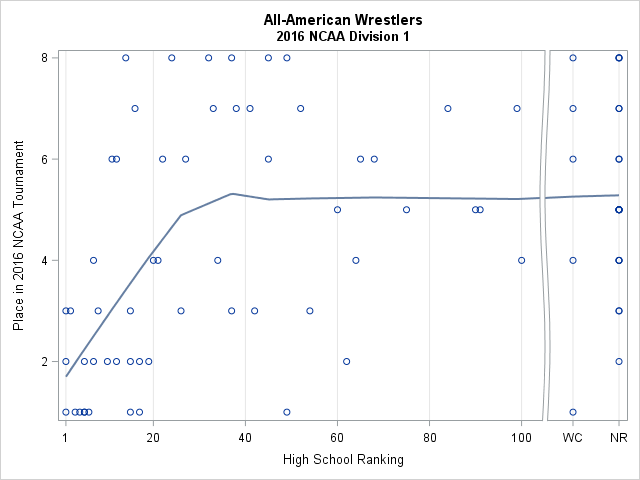
The scatter plot of place versus high school ranking is shown to the left, along with a loess smoother to the data. In order to separate these artificial ranks from the real ranks, I create a broken axis on the graph. The graph indicates that the All-Americans who were very highly ranked in high school placed very well at the NCAA tournament. For example, 14 wrestlers were ranked in the Top 10 in high school. Of those, 10 wrestled in the finals for first or second place, and another four wrestled for third or fourth place.

The association between place and ranking is noticeable until about ranking 25. After that, the loess smoother levels off, which indicates no relationship between high school ranking and placement at the tournament.

I want to emphasize that this sample is not a random selection of collegiate wrestlers. Because of that, you cannot conclude that high school ranking predicts success in college wrestling. The sample here is nonrandom. Therefore the graphs show a relationships given that these men are All-American champions. It is a subtle but important distinction.

Feel free to download the SAS program that created these graphs. Although in general I am not a fan of broken axes, I think they are useful in this case because it makes it clear that the ranks 1–100 are different from the ranks "WC" and "NR". See Sanjay Matange's blog for more conventional applications of broken axes.

This analysis sends a clear message to high school wrestlers who are not nationally ranked: With hard work you can still become a premier collegiate athlete. At the same time, it clearly supports another truism: Many of the best athletes in college were also high school stars.