Many people enjoy solving word games such as the daily Cryptoquote puzzle, which uses a simple substitution cipher to disguise a witty or wise quote by a famous person. A common way to attack the puzzle is frequency analysis. In frequency analysis you identify letters and pairs of letters (bigrams) that occur often in the enciphered text. It is a fact that certain letters (e, t, a, o, i, n,....) and bigrams (th, he, in, er, an, re, on,...) appear frequently in English text. You can use this fact to guess that the most frequently occurring symbol in the text might represent e, t, or a. You can use the bigram frequencies in the text to help you make statistically likely guesses.
Usually frequency analysis is used for the initial guesses. Soon recognizable snippets of words begin to appear in the partially deciphered text, and you can often guess small words such as 'the', 'and', 'of', and 'for'. Then, like pulling a string on a sweater, the puzzle unravels. Use the context of the message to guess the remaining letters.
This article shows how to use frequency analysis to solve a cryptogram. I use a computer program to count the frequency of letters and bigrams and to quickly substitute guessed letters into the puzzle. However, the computer program merely provides an implementation of a tedious and repetitive task. You can perform the same analysis with pencil and paper. The program does not make any guesses itself, but merely makes it easier for a human to make a guess. (Type 'cryptogram solver' into an internet seach engine if you want an online solver.)
I use the convention that capital letters are symbols for the enciphered text whereas lowercase letters indicate the plaintext. Thus the plaintext message "word games are fun" might be enciphered as "RHES ADLUI DEU VYP." A partially deciphered solution might appear as "RHrS AaLeI are VYn," where the uppercase letters represent yet-to-be-solved letters.
Some functions that help decipher Cryptoquotes
In this blog I usually discuss statistical programming in the SAS/IML language. This post uses statistics and programming, but the discussion is about deciphering the Cryptoquote. The program that I use in this article is available for download for SAS users who have access to SAS/IML software. I wrote the following SAS/IML functions:
- The PrintFreqRef routine prints reference tables that show how often certain letters and pairs of letters appear in English text. The tables are the results from previous blog posts and show the most frequently appearing letters, the most frequent bigrams, and the most frequent double-letter bigrams.
- The FreqAnalysis routine reports the distribution of letters, bigrams, and double letters in the enciphered quote.
- The SplitByWords function constructs an array from a quote. Each word is on one row; each letter is in a separate column. The main purpose of this routine is so that I can say "look at the 7th word" and you will be able to find it easily.
- The ApplySubs function enables you to quickly see the result of replacing one or more cipher symbols with a guess. You can use the function to replace 'Q' with 't' and 'F' with 'e' and see whether the substitutions appear to make sense in the quote. If the substitution results in nonsense—such as 'te' as a two-letter word—then the substitution was not good and you can try a different guess.
Solving the Cryptoquote by using frequency analysis
The following statements start PROC IML, load the utility modules, and print the reference tables that show the expected frequencies of letters and bigrams in English text.
proc iml; load module=_all_; /* load the utility modules */ run PrintFreqRef(); |
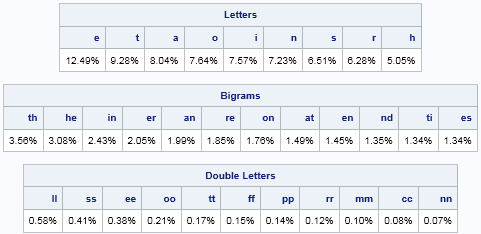
The reference tables show the relative frequencies of the most common letters, such as e, t, a, o, i, n, and s. The most frequent pairs of letters are th, he, in, er, and so forth. The most common double-letter bigrams are ll, ss, ee, oo, and so forth. If you like to solve word puzzles by pencil and paper, you can print this table and keep a copy in your wallet or purse. Click the table to get it to appear on a separate web page.
Now let's look at an enciphered quote and perform a frequency analysis on its symbols:
msg = "KBSCS OCS KPUSH XBSW DOCSWKBTTG HSSUH WTKBPWJ " +
"IAK LSSGPWJ KBS UTAKB KBOK IPKSH MTA. " +
"~ DSKSC GS FCPSH";
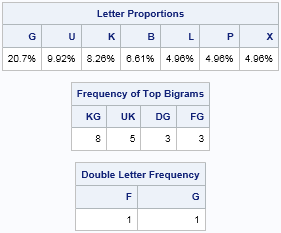
run FreqAnalysis(msg); |
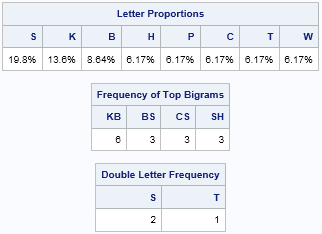
These tables look similar to the reference tables, but these tables are specific to this quote. You can create these table by hand if you have the time and patience. In this quote, almost 20% of the symbols are an S. The next most frequent symbols are K and B. Furthermore, the bigrams KB and BS appear frequently. This co-occurrence of three symbols and two bigrams is a "trifecta" that gives strong statistical evidence that S=e, K=t, and B=h. The S=e guess is further supported by the fact that SS appears twice in the message, and 'ee' is a common double-letter bigram.
Let's make the substitutions:
w = SplitByWords(msg); /* split into array */
rownum = char(1:nrow(w)); /* row numbers, for reference */
w1 = ApplySubs(w, {K B S}, {t h e}); /* guess K=t, B=h, and S=e */
print w1[r=rownum]; |
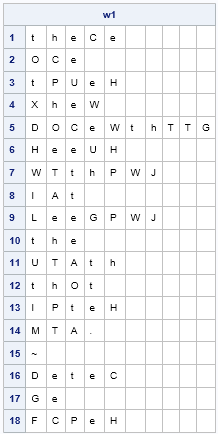
It looks like we made a great guess! The first word is probably 'there', so the next substitution should include C=r. This guess is bolstered by the fact that CS appears several times in this message, and 're' is a frequent bigram. (The first word could also be 'these', but 'se' occurs less often than 're'.)
If that guess is correct, then we can further guess that O=a because that makes the second word 'are' and the 12th word 'that'.
To generate another guess, notice that the double-letter bigram TT appears in this quote in the 5th word. The bigram follows the plaintext bigram 'th', so TT must represent a double vowel. Because we have already deduced the symbol for 'e', we guess that TT is 'oo', which is the only other common double-vowel bigram. Therefore T=o.
Lastly, the 16th word is the author's first name. Since C=r, we guess that the first name might be 'peter'. The following statement makes these substitutions:
w2 = ApplySubs(w1, {O C}, {a r});
w3 = ApplySubs(w2, {T D}, {o p});
print w3[r=rownum]; |
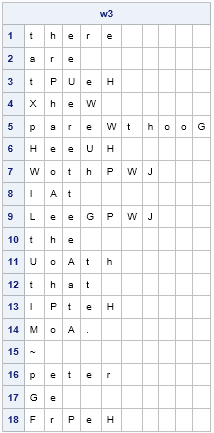
Frequency analysis can suggest additional guesses. The symbols H, P, and W appear frequently in the enciphered quote. We also see that SH (=eH) is a frequent bigram. From the bigram frequency analysis, we might guess that H=n or H=s. By looking at the partially deciphered quote, it looks like W=n because the 5th word is probably 'parenthood', so we will guess H=s.
By looking at where the symbol P appears in the quote, you might guess that P is a vowel. The remaining vowel that occurs frequently is 'i'. This guess makes sense because the trigram PWJ appears twice, and this trigram could be 'ing'.
The following statement make these substitutions.
w4 = ApplySubs(w3, {H W G P J}, {s n d i g});
print w4[r=rownum]; |
Click this link to see the partially deciphered text that results from these substitutions. At this point, frequency analysis has revealed all but seven of the symbols in the enciphered quote. The remaining symbols are easily deduced by looking at the partially deciphered words and guessing the remaining letters. The deciphered quote is:
There are times when parenthood seems nothing but feeding the mouth that bites you.
~ Peter de Vries
Frequency analysis enabled us to guess values for certain frequently occurring symbols. By correctly guessing these key symbols, the puzzle was solved. Notice that the frequency of bigrams was essential in this process. If you use only the frequency of single letters, you might be able to guess the 'e' and 't', but the other letters are indistinguishable by looking at the empirical frequencies. However, by using bigrams, you can guess more symbols. For example, in this puzzle the bigrams helped us to discover the symbols for 'h', 'o', 's', and 'n'.
Of course, this process is not always linear. Sometimes you will make a guess that turns out to be wrong. In that case, eliminate the wrong guess and try another potential substitution.
To conclude this article, I will leave you with another Cryptoquote. I will generate the frequency analysis for you, in case you want to solve the puzzle by hand. You can download the SAS/IML program that deciphers this quote. The program contains comments that explain how frequency analysis is used to solve the puzzle.
CG EKLVFX WLU MVXZG IGLIFG YH UKGSB IGPQ LR GNDGFFGWDG; YVU YH UKG XSEUPWDG UKGH KPTG UBPTGFGX RBLA UKG ILSWU CKGBG UKGH EUPBUGX.
~ KGWBH CPBX YGGDKGB
