
Last week I showed three ways to sample with replacement in SAS. You can use the SAMPLE function in SAS/IML 12.1 to sample from a finite set or you can use the DATA step or PROC SURVEYSELECT to extract a random sample from a SAS data set. Sampling without replacement is similar. This article describes how to use the SAS/IML SAMPLE function or the SURVEYSELECT procedure.
Simulate dealing cards
When I wrote about how to generate permutations in SAS, I used the example of dealing cards from a standard 52-card deck. The following SAS/IML statements create a 52-element vector with values 2H, 3H, ..., KS, AS, where 'H' indicates the heart suit, 'D' indicates diamonds, 'C' indicates clubs, and 'S' indicates spades:
proc iml;
/* create a deck of 52 playing cards */
suits52 = rowvec( repeat({H, D, C, S},1,13) );
vals = char(2:10,2) || {J Q K A};
vals52 = repeat( right(vals), 1, 4 );
Cards = vals52 + suits52;
/* choose 20 cards without replacement from deck */
call randseed(293053001);
deal = sample(Cards, 20, "WOR"); /* sample 20 cards without replacement */ |
The third argument to the SAMPLE function is the value "WOR", which stands for "without replacement." With this option, the SAMPLE function returns 20 cards from the deck such that no card appears more than once in the sample. If there are four card players who are playing poker and each gets five cards, you can use the SHAPE function to reshape the 20 cards into a matrix such that each column indicates a player's poker hand:
PokerHand = shape(deal, 0, 4); /* reshape vector into 4 column matrix */
print PokerHand[c=("Player1":"Player4")]; |
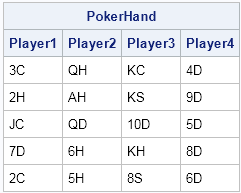
Let's see what poker hands these players were dealt. The first player has a pair of 2s. The second player has a pair of queens. The third player has three kings, and the fourth player has a flush! That was a heck of a deal! (I'll leave it to the sharp-eyed reader to figure out how I "cheated" in order to simulate such an improbable "random" sample. Extra credit if you link to a blog post of mine in which I explain the subterfuge.)
The SAMPLE function provides a second way to sample without replacement. If the third argument is "NoReplace", then a faster algorithm is used to extract a sample. However, the sample is in the same order as the original elements, which might not be acceptable. For the poker example, the "WOR" option enables you to simulate a deal. If you use the "NoReplace" option, then you should first use the RANPERM function to shuffle the deck. Of course, if you only care about the sample as a set rather than as a sequence, then using the faster algorithm makes sense.
One more awesome feature of the SAMPLE function: it enables you to sample with unequal probabilities by adding a fourth argument to the function call.
Sampling without replacement by using the SURVEYSELECT procedure
As mentioned above, some algorithms generate a sample whose elements are in the same order as the original data. This is the case with the SURVEYSELECT procedure when you use the METHOD=SRS option. Suppose that you write the 52 cards to a SAS data set. You can use the SURVEYSELECT procedure to extract 20 cards without replacement, as follows:
create Deck var {"Cards"}; append; close Deck; /* create data set */
quit;
proc surveyselect data=Deck out=Poker seed=1
method=srs /* sample w/o replacement */
sampsize=20; /* number of observations in sample */
run;
proc print data=Poker(obs=8); run; |
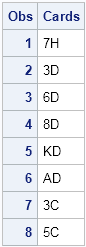
The output shows the first eight observations in the sample. You can see that the hearts appear first, followed by the diamonds, followed by the clubs, and that within each suit the values of the cards are in their original order. If you want the data in a random order, imitate the DATA step code in the SAS Knowledge Base article "Simple Random Sample without Replacement."

6 Comments
Pingback: Twelve posts from 2014 that deserve a second look - The DO Loop
For some reason, the final link above, to the excellent SAS Knowledge Base article "Simple Random Sample without Replacement" http://support.sas.com/kb/24/722.html no longer works.
Strange. Perhaps someone was doing some maintenance. I found another KB article with the same title, but a differnt number: 24/802
Pingback: Four essential sampling methods in SAS - The DO Loop
I suppose you "cheated" by not shuffling the deck and with the randseed call somehow you took advantage of knowledge about the ordered deck you had created.
:-) Close! I just tried many seeds until I found one that gave an "unusual" deal. The seed 293053001 was certainly not the first seed I tried!