This article is an excerpt from my forthcoming book Simulating Data with SAS.

Not every matrix with 1 on the diagonal and off-diagonal elements in the range [–1, 1] is a valid correlation matrix. A correlation matrix has a special property known as positive semidefiniteness. All correlation matrices are positive semidefinite (PSD), but not all estimates are guaranteed to have that property. For example, robust estimators and matrices of pairwise correlation coefficients are two situations in which an estimate might fail to be PSD.

A third situtation can occur when a correlation matrix is estimated based on forecasts. For example, an analyst might conjecture that the correlation between certain currencies (such as the dollar, yen, and euro) will have certain values in the coming year:

• the first and second currencies will have correlation R₁₂ = 0.6.
• the first and third currencies will have correlation R₁₃ = 0.9.
• the second and third currencies will have correlation R₂₃ = 0.9.

Unfortunately, the resulting matrix of pairwise correlations is not positive definite and therefore does not represent a valid correlation matrix. How can you tell? Positive semidefinite matrices always have nonnegative eigenvalues. As shown by the output of following program, this matrix has a negative eigenvalue:

proc iml;
R = {1.0 0.6 0.9,
     0.6 1.0 0.9,
     0.9 0.9 1.0};
eigval = eigval(R);
print eigval;

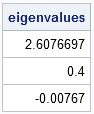
So there you have it: a matrix of correlations that is not a correlation matrix. Mathematically, the problem is that the various correlations between variables are not independent, which means that analyst cannot choose pairwise correlations arbitrarily. If R is a correlation matrix, then the correlations must satisfy the condition det(R) ≥ 0. For a 3 x 3 matrix, this implies that the correlation coefficients satisfy the equation:

R²₁₂ + R²₁₃ + R²₂₃ - 2 R₁₂ R₁₃ R₂₃ ≤ 1

The set of (R₁₂, R₁₃, R₂₃) triplets that satisfy the inequality forms a convex subset of the unit cube, as shown in the following image, which is from Rousseeuw and Molenberghs (TAS, 1994).

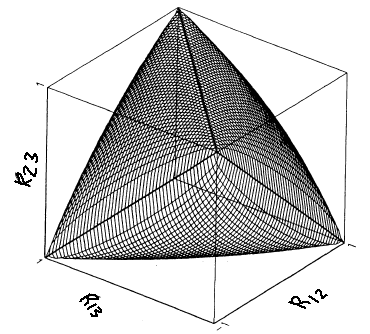
If you substitute the values R₁₂=0.6 and R₁₃ = R₂₃ = 0.9, you discover that these three values do not satisfy the inequality. The triplet of pairwise correlations is outside of the convex region shown in the figure.

This can cause problems in multivariate analyses and simulation studies. But what can you do about it? One solution is to try to find a valid correlation matrix that is closest (in some sense) to your estimate.

In my book, I provide SAS/IML functions that implement an algorithm due to Nick Higham that finds the closest correlation matrix by projecting the estimate onto the surface of the convex region. The algorithm works in arbitrary dimensions.

This is a good time to remind SAS users that by default PROC CORR computes pairwise correlations. If your variables contain missing values, the resulting matrix of correlations might not be PSD. If you intend to use the PROC CORR output for simulation or as input for a regression or multivariate analysis, be sure to specify the NOMISS option on the PROC CORR statement! This option excludes observations with missing values and always results in a positive semidefinite estimate of correlation.