Sorting is a fundamental operation in statistical programming, and most SAS programmers are familiar with PROC SORT for sorting data sets. But did you know that you can also sort rows of a SAS/IML matrix according to the value of one or more columns? This post shows how.

Sorting a Matrix In-Place

Not surprisingly, the SAS/IML subroutine that sorts a matrix is the SORT subroutine.

You can sort a matrix by the values in any column or set of columns. You can also specify whether the values in a column should be sorted in ascending or descending order. For example, the following statements sort a matrix by the first column:

proc iml;
x = {5 1 4,
     1 5 1,
     4 3 4,
     2 4 3,
     2 3 1,
     3 2 3};
call sort(x, 1); /** sort x by 1st col **/
print x;

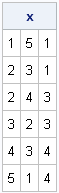
Notice that the matrix x is overwritten by the result. That is, the SORT subroutine sorts the rows of the matrix "in place." In SAS/IML 9.22, the second argument is optional and defaults to 1. Therefore, you can use a simpler statement, call sort(x), to sort a matrix by the first column.

Rows with the same value of the specified column (such as rows 4 and 5 of the original x matrix, which both have a 2 in the first column) appear in the sorted matrix in arbitrary order.

Sorting a Matrix by Values in Multiple Columns

By default, the matrix is sorted so that the specified columns are in ascending order. To sort a matrix in descending order, specify one or more column numbers as the third argument to the SORT subroutine. For example, the following statements sort the rows of the matrix by two columns. The third column is sorted in descending order and ties are broken by sorting the second column in ascending order.

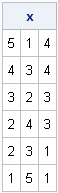
/** sort by 3rd col (descending) and 2nd col **/
call sort(x, {3 2}, 3);
print x;

Sorting a Matrix without Overwriting It

There might be times when you do not want to overwrite a matrix with the sorted version of the matrix. Perhaps you only need to know which row is first in the sorted order. In this case, you can use the SORTNDX subroutine, which returns a vector that contains the row numbers that will sort the matrix. The following statements call the SORTNDX function and print the vector of row numbers:

x = {5 1 4,
     1 5 1,
     4 3 4,
     2 4 3,
     2 3 1,
     3 2 3};
/** get row numbers that sort the matrix **/
call sortndx(idx, x, 1);
print idx;

The idx vector indicates that row 2 is the first row in the sorted matrix, row 5 is the second row in the sorted matrix, and so on, down to row 1, which is the last row in the sorted matrix.

If you want to explicitly sort the x matrix, you can use the idx vector as a row subscript:

y = x[idx, ]; /** y is sorted version of x **/