Suppose that you compute the coefficients of a polynomial regression by using a certain set of polynomial effects and that I compute coefficients for a different set of polynomial effects. Can I use my coefficients to find your coefficients? The answer is yes, and this article explains how.

Standard Polynomial Regression

Suppose that you compute a regression model of a response variable, Y, by using polynomials in a single variable, X. Typically, low-order polynomials are used, such as second-degree (quadratic) or third-degree (cubic) polynomials. This example uses third-degree polynomials.

Frequently, the standard monomials (1, x, x², x³) are used as basis functions for the regression. (Here basis is used in the linear algebraic sense to mean a basis for a vector space.) That is, the columns of the design matrix are formed by evaluating each monomial on the data. The regression produces coefficients c0, c1, c2 and c3 such that the linear combination c0 + c1 x + c2 x² + c3 x³ is the best fit to the Y data in the least squares sense. In PROC IML, you can find the coefficients by solving the normal equations as shown in the following example:

proc iml;
x = T(do(-1,1,0.2));
y = {6,8,8,7,5,3,2,1,3,6,10};  /** observed data x and y **/ 
 
/** define standard polynomial basis **/
Intercept = j(nrow(x), 1, 1);
B1 = Intercept || x || x##2 || x##3;
 
/** compute parameter estimates by solving normal equations **/
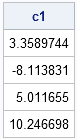
c1 = inv(B1` * B1) * (B1` * y);
print c1;

Polynomial Regression with an Alternate Basis

Suppose that I use a different basis for my regression, such as (1, x, (3x² - 1)/2, (5x³-3x)/2). This might be done for various reasons such as computational efficiency, numerical stability, or ease of interpreting the resulting coefficients.

Programmatically, I can compute the regression coefficients (parameter estimates) for my polynomial basis by using the above technique: evaluate the polynomials on the data to form the design matrix and use the method of normal equations to solve for the coefficients:

/** define alternate basis; solve normal equations **/
B2 = Intercept || x || (3*x##2 - 1)/2 || (5*x##3-3*x)/2;
c2 = inv(B2` * B2) * (B2` * y);
print c2;

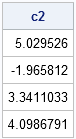
Note that my coefficients are different than yours, because I used different basis functions, but they both represent exactly the same least squares solution.

The question is: If I know my regression coefficients, can I use them to find yours? In other words, if I know c2 and which basis functions we each used, can I find c1? Absolutely!

Changing Bases

To find your regression coefficients, all I have to do is to write my basis functions in terms of your basis functions. In matrix terms, I can write down the transition matrix that expresses my basis functions in terms of your monomials:

/** Transition matrix that expresses basis B2 in terms of B1 **/
S = {1  0  -0.5     0,
     0  1     0  -1.5,
     0  0   1.5     0,
     0  0     0   2.5};

The jth column of S expresses the jth function in the B2 basis in terms of the functions in the B1 basis. The first column specifies that the first basis function in B2 is the same as the first basis function in B1. The second column specifies that x (the second basis function in B2) is equal to the second basis function in B1. The third column expresses (3x² - 1)/2 as a linear combination of the first and third basis functions in B1, and the last column represents (5x³-3x)/2. The transition matrix expresses each element in the B2 basis as a linear combination of the B1 basis functions. In matrix terms, B2 = B1*S, as shown by the following SAS/IML statements:

/** show that B2 = B1*S **/
diff = B1*S - B2;
maxDiff = (max(abs(diff))); 
reset fuzz; print maxDiff;

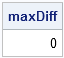
The transition matrix makes it easy to find the regression coefficients in the standard basis. I simply multiply my coefficients, c2, by the transition matrix to obtain the coefficients in the B1 basis:

/** Given c2, find c1 **/
c1 = S * c2; 
print c1;

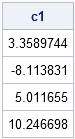
In particular, after I compute regression coefficients in one polynomial basis, I can find the regression coefficients for any other basis without re-solving the normal equations. All I have to do is write down the transition matrix and use matrix multiplication.