When you analyze data, you will occasionally have to deal with categorical variables. The typical situation is that you want to repeat an analysis or computation for each level (category) of a categorical variable. For example, you might want to analyze males separately from females.
Unlike most other SAS procedures, PROC IML does not have a BY statement for repeating an analysis. When you analyze data by using the SAS/IML language, there is a little trick (actually, a technique) that helps you analyze data by category. I call it the UNIQUE-LOC technique, and wrote about it Section 3.3.5 of my book, Statistical Programming with SAS/IML Software.
Analyzing categories in SAS/IML software
To be concrete, suppose that you want to compute the mean for the heights of males and females (separately) in the Sashelp.Class data set. Of course, you could use PROC MEANS for this simple statistic, but let's see what it would look like in the SAS/IML language. To compute a statistic for each category, do the following:
- Read in the data by using the USE and READ statements. So that the UNIQUE-LOC technique can be easily reused (and is not tied to the Sashelp.Class data), read the categorical variable (SEX) into the vector C and read a numeric variable (HEIGHT) into the vector x.
- Use the UNIQUE function to obtain the unique values (levels) of the categorical variable.
- Allocate a vector to hold the statistics, one for each level.
- Use a DO loop to iterate over the unique values.
- For the ith level of the categorical variable, use the LOC function to find the observations in the level.
- Extract the corresponding numerical values, and compute the statistic for those values.
The following SAS/IML statements implement the UNIQUE-LOC technique:
proc iml;
use sashelp.class; /* 1. Read in the data */
read all var {sex} into C; /* categorical variable, C */
read all var {height} into x; /* numerical variable, x */
close;
u = unique(C); /* 2. Unique values (levels) of categorical variable. */
s = j(1, ncol(u)); /* 3. Allocate vector to hold results */
do i = 1 to ncol(u); /* 4. For each level... */
idx = loc(C=u[i]); /* 5. Find observations in level */
s[i] = mean(x[idx]);/* 6. Compute a statistic for those values */
end;
print s[colname=u]; /* assumes that u is character vector */ |
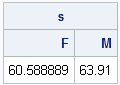
Notice in Step 6 that the quantity x[idx] contains the values of the numerical value for a given level of the categorical variable. For complicated computations, it might be helpful to physically extract those values: y = x[idx];
Although this example uses a character categorical variable, the algorithm also works for numerical categorical variables. However, the PRINT statement needs to be modified:
lbl = putn(u, "Best4."); /* if u is numerical, convert to char */ print s[colname=lbl]; |
If you are computing is the number of observations in each category, you can eliminate the DO loop and use the TABULATE function (new in SAS 9.3), which is more efficient. The TABULATE function finds the unique values of the categorical variable and counts the number of observations for each value:
call tabulate(u, count, C); /* find unique values and count obs */ |

17 Comments
Hi, Rick. I am a PhD student studying data mining. Right now I hope to apply Support Vector Machine (SVM) on a large-scale dataset in SAS. I need to solve a large scale quadratic optimization problem, and I think SAS/IML should be the best option. However, the problem is I still don't know how to programme with it. For example, in Matlab, if you have an optimization problem as follows:
min (1/2)*x'Hx+q'x
s.t. A*x<=b
Aeq*x=beq
l<=x<=u
where H, A, Aeq are matrices, and q, b, beq, l, u are vectors. As long as define the above matrices and vector and input them in a MatLab function, the problem can be solved. So I wonder if there is such a function in SAS/IML. I am really appreciated for your reply. Thank you so much.
For "large scale" data, you might need more specialized tools.
I suggest that you ask this question at the SAS Data Mining Forum:
http://communities.sas.com/community/sas_data_mining_and_text_mining
If you want to solve large quadratic programming problems, then PROC OPTMODEL in SAS/OR software is your best bet. You can ask SAS/OR questions at http://communities.sas.com/community/mathematical_optimization_and_operations_research_with_sas
thank you for that !
Pingback: Reshape data so that each category becomes a new variable - The DO Loop
Pingback: Recoding a character variable as numeric - The DO Loop
Pingback: BY-group processing in SAS/IML - The DO Loop
There may also be many circumstances in which the do loop can be eliminated by using the 'design' function. For example try adding the line:
print (choose(design(C),repeat(x,1,ncol(u)),.)[:,]) [colname=u];
to the program above to calculate both means in one statement. Which makes me think it would be a good idea if there was a way for the design function to return the list of unique values in sorted order, it must have this internally, so it would be nice to get at it, and not have to calculate it again with the 'unique' function.
See if the UNIQUEBY call satisfies your needs. I blogged about the UNIQUEBY function in my article "An efficient alternative to the UNIQUE-LOC technique."
Hi Rick,
I took your Simulation continuing education course at JSM 2012. I am trying out the code, containing "call tabulate". I have SAS 9.2 and as I am learning, "call tabulate" does not work in that version. Can you expound more in using this Unique-Loc trick as an alternative. The example you outlined in this blog is if you have a data with character and numeric variables. How about in your JSM course example when you only have a single column of coin toss outcome (page 45 of your slides). Thanks in advance.
Define and call the following function:
/* alternate approach */ start MyTabulate(levels, freq, x); levels = unique(x); freq = j(1, ncol(levels)); do i = 1 to ncol(levels); freq[i] = sum(x = levels[i]); end; finish;Pingback: Designing a quantile bin plot - The DO Loop
Pingback: Group processing in SAS: The NOTSORTED option - The DO Loop
Pingback: Matrix operations and BY groups - The DO Loop
Hi Rick, Does IML support the case when there is more than one categorical variable and we need sums grouped by all categorical variables together? Thanks!
Yes. Look at the UNIQUEBY function, which enables you to group by multiple variables.
Pingback: Use design matrices to analyze subgroups in SAS IML - The DO Loop
Pingback: Programming the formulas for an ANOVA in SAS - The DO Loop